信用卡客户划分

本文对信用卡客户数据进行聚类分析。先处理数据，删除无关ID，填补缺失值，对偏斜数据做对数转换。接着用PCA降维保留95%方差。通过肘部法和轮廓得分，选择2或3个聚类数，用KMeans聚类。结果显示，2类可分高低使用率客户，3类细分更优，能为营销策略提供依据。

信用卡客户划分

作者: https://www.kaggle.com/muhammadzubairkhan92

译者: 我

---

本数据集所描述的问题要求我们根据数据集中提供的客户行为模式，提取出客户的细分市场，将企业的营销策略集中于某一细分市场。

In [17]

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as sns

登录后复制    

加载数据

In [18]

df = pd.read_csv('/home/aistudio/data/data82416/Credit Card Dataset for Clustering.csv')

登录后复制    In [19]

df.head()

登录后复制        

  CUST_ID      BALANCE  BALANCE_FREQUENCY  PURCHASES  ONEOFF_PURCHASES  \0  C10001    40.900749           0.818182      95.40              0.00   1  C10002  3202.467416           0.909091       0.00              0.00   2  C10003  2495.148862           1.000000     773.17            773.17   3  C10004  1666.670542           0.636364    1499.00           1499.00   4  C10005   817.714335           1.000000      16.00             16.00      INSTALLMENTS_PURCHASES  CASH_ADVANCE  PURCHASES_FREQUENCY  \0                    95.4      0.000000             0.166667   1                     0.0   6442.945483             0.000000   2                     0.0      0.000000             1.000000   3                     0.0    205.788017             0.083333   4                     0.0      0.000000             0.083333      ONEOFF_PURCHASES_FREQUENCY  PURCHASES_INSTALLMENTS_FREQUENCY  \0                    0.000000                          0.083333   1                    0.000000                          0.000000   2                    1.000000                          0.000000   3                    0.083333                          0.000000   4                    0.083333                          0.000000      CASH_ADVANCE_FREQUENCY  CASH_ADVANCE_TRX  PURCHASES_TRX  CREDIT_LIMIT  \0                0.000000                 0              2        1000.0   1                0.250000                 4              0        7000.0   2                0.000000                 0             12        7500.0   3                0.083333                 1              1        7500.0   4                0.000000                 0              1        1200.0         PAYMENTS  MINIMUM_PAYMENTS  PRC_FULL_PAYMENT  TENURE  0   201.802084        139.509787          0.000000      12  1  4103.032597       1072.340217          0.222222      12  2   622.066742        627.284787          0.000000      12  3     0.000000               NaN          0.000000      12  4   678.334763        244.791237          0.000000      12

登录后复制                In [20]

df.describe()

登录后复制        

            BALANCE  BALANCE_FREQUENCY     PURCHASES  ONEOFF_PURCHASES  \count   8950.000000        8950.000000   8950.000000       8950.000000   mean    1564.474828           0.877271   1003.204834        592.437371   std     2081.531879           0.236904   2136.634782       1659.887917   min        0.000000           0.000000      0.000000          0.000000   25%      128.281915           0.888889     39.635000          0.000000   50%      873.385231           1.000000    361.280000         38.000000   75%     2054.140036           1.000000   1110.130000        577.405000   max    19043.138560           1.000000  49039.570000      40761.250000          INSTALLMENTS_PURCHASES  CASH_ADVANCE  PURCHASES_FREQUENCY  \count             8950.000000   8950.000000          8950.000000   mean               411.067645    978.871112             0.490351   std                904.338115   2097.163877             0.401371   min                  0.000000      0.000000             0.000000   25%                  0.000000      0.000000             0.083333   50%                 89.000000      0.000000             0.500000   75%                468.637500   1113.821139             0.916667   max              22500.000000  47137.211760             1.000000          ONEOFF_PURCHASES_FREQUENCY  PURCHASES_INSTALLMENTS_FREQUENCY  \count                 8950.000000                       8950.000000   mean                     0.202458                          0.364437   std                      0.298336                          0.397448   min                      0.000000                          0.000000   25%                      0.000000                          0.000000   50%                      0.083333                          0.166667   75%                      0.300000                          0.750000   max                      1.000000                          1.000000          CASH_ADVANCE_FREQUENCY  CASH_ADVANCE_TRX  PURCHASES_TRX  CREDIT_LIMIT  \count             8950.000000       8950.000000    8950.000000   8949.000000   mean                 0.135144          3.248827      14.709832   4494.449450   std                  0.200121          6.824647      24.857649   3638.815725   min                  0.000000          0.000000       0.000000     50.000000   25%                  0.000000          0.000000       1.000000   1600.000000   50%                  0.000000          0.000000       7.000000   3000.000000   75%                  0.222222          4.000000      17.000000   6500.000000   max                  1.500000        123.000000     358.000000  30000.000000              PAYMENTS  MINIMUM_PAYMENTS  PRC_FULL_PAYMENT       TENURE  count   8950.000000       8637.000000       8950.000000  8950.000000  mean    1733.143852        864.206542          0.153715    11.517318  std     2895.063757       2372.446607          0.292499     1.338331  min        0.000000          0.019163          0.000000     6.000000  25%      383.276166        169.123707          0.000000    12.000000  50%      856.901546        312.343947          0.000000    12.000000  75%     1901.134317        825.485459          0.142857    12.000000  max    50721.483360      76406.207520          1.000000    12.000000

登录后复制                In [21]

df.info()

登录后复制        

RangeIndex: 8950 entries, 0 to 8949Data columns (total 18 columns): #   Column                            Non-Null Count  Dtype  ---  ------                            --------------  -----   0   CUST_ID                           8950 non-null   object  1   BALANCE                           8950 non-null   float64 2   BALANCE_FREQUENCY                 8950 non-null   float64 3   PURCHASES                         8950 non-null   float64 4   ONEOFF_PURCHASES                  8950 non-null   float64 5   INSTALLMENTS_PURCHASES            8950 non-null   float64 6   CASH_ADVANCE                      8950 non-null   float64 7   PURCHASES_FREQUENCY               8950 non-null   float64 8   ONEOFF_PURCHASES_FREQUENCY        8950 non-null   float64 9   PURCHASES_INSTALLMENTS_FREQUENCY  8950 non-null   float64 10  CASH_ADVANCE_FREQUENCY            8950 non-null   float64 11  CASH_ADVANCE_TRX                  8950 non-null   int64   12  PURCHASES_TRX                     8950 non-null   int64   13  CREDIT_LIMIT                      8949 non-null   float64 14  PAYMENTS                          8950 non-null   float64 15  MINIMUM_PAYMENTS                  8637 non-null   float64 16  PRC_FULL_PAYMENT                  8950 non-null   float64 17  TENURE                            8950 non-null   int64  dtypes: float64(14), int64(3), object(1)memory usage: 1.2+ MB

登录后复制        In [22]

df.isna().mean()*100

登录后复制        

CUST_ID                             0.000000BALANCE                             0.000000BALANCE_FREQUENCY                   0.000000PURCHASES                           0.000000ONEOFF_PURCHASES                    0.000000INSTALLMENTS_PURCHASES              0.000000CASH_ADVANCE                        0.000000PURCHASES_FREQUENCY                 0.000000ONEOFF_PURCHASES_FREQUENCY          0.000000PURCHASES_INSTALLMENTS_FREQUENCY    0.000000CASH_ADVANCE_FREQUENCY              0.000000CASH_ADVANCE_TRX                    0.000000PURCHASES_TRX                       0.000000CREDIT_LIMIT                        0.011173PAYMENTS                            0.000000MINIMUM_PAYMENTS                    3.497207PRC_FULL_PAYMENT                    0.000000TENURE                              0.000000dtype: float64

登录后复制                

从报告中我们可以看到，大多数特征的平均值远远大于其中位数。这说明数据集中有一定的数据偏移，我们要看看是否可以做些什么。

我们还有一些Nan值要进行处理。

数据处理

客户ID似乎是每个客户的唯一ID，因此不会在确定集群中起到任何作用。

In [23]

df.drop(['CUST_ID'], axis=1, inplace=True)

登录后复制    

我们看到，信用额度功能只有0.01%的记录是Nan值，即这里只有1条记录有缺失值。所以我们不必费心去推算它。我们可以直接放弃它，再也不用考虑它了。

In [24]

df.dropna(subset=['CREDIT_LIMIT'], inplace=True)

登录后复制    

对于估算最低支付额的特征，我没有看到任何一列与这个特征有关的，可以帮助我们估算缺失记录的值。似乎这些值是随机缺失的，我们可以简单地使用中值来代替Nan值，因为最低支付额的分布是倾斜的，因此中值可以更好地估计这个特征的中心倾向。

In [25]

df['MINIMUM_PAYMENTS'].fillna(df['MINIMUM_PAYMENTS'].median(), inplace=True)

登录后复制    

如果我们不可视化，我们还算是数据科学家吗？

让我们来可视化一下我, 看看该数据集有多偏斜。

In [26]

plt.figure(figsize=(20,35))for i, col in enumerate(df.columns):    if df[col].dtype != 'object':        ax = plt.subplot(9, 2, i+1)        sns.kdeplot(df[col], ax=ax)        plt.xlabel(col)        plt.show()

登录后复制        

登录后复制                

哇！！！有很多数据都是严重偏离的，而且它们是不同的。这符合我们预期，因为总会有一些客户有着非常高的交易量。

现在，这取决于我们的应用是否要处理数据集中的偏度问题。例如，如果我们想做聚类检测，在这种情况下，我们不想处理异常值，因为我们希望我们的模型能够检测到它们，并将它们分组。对于我们的应用，我正在寻找一个良好的可视化，所以我希望尽可能地处理偏度，因为它将帮助模型形成更好的聚类。

让我们看看我们是否可以在这方面做些什么。

In [27]

cols = ['BALANCE', 'ONEOFF_PURCHASES', 'INSTALLMENTS_PURCHASES', 'CASH_ADVANCE', 'ONEOFF_PURCHASES_FREQUENCY','PURCHASES_INSTALLMENTS_FREQUENCY', 'CASH_ADVANCE_TRX', 'PURCHASES_TRX', 'CREDIT_LIMIT', 'PAYMENTS', 'MINIMUM_PAYMENTS', 'PRC_FULL_PAYMENT']

登录后复制    In [28]

for col in cols:    df[col] = np.log(1 + df[col])

登录后复制    In [29]

plt.figure(figsize=(15,20))for i, col in enumerate(cols):    ax = plt.subplot(6, 2, i+1)    sns.kdeplot(df[col], ax=ax)plt.show()

登录后复制        

登录后复制                

我知道这可能看起来不像一个理想的分布，但它比刚才强一些了，作为数据科学家，我们的工作是尽可能地帮助我们的模型。

现在试着寻找一些关联性。

In [30]

plt.figure(figsize=(12,12))sns.heatmap(df.corr(), annot=True)plt.show()

登录后复制        

登录后复制                

我们已经有了一些相关的功能。有很多方法可以处理这个问题。我们会继续进行维度降低，我们会把我们的数据降到低维。

我们会使用PCA来进行降维。

简单地解释一下PCA的工作原理，就是为数据集找到新的维度/轴，使它能解释最大的方差。这个轴就是第一个主成分。然后它选择另一个垂直于第一主成分的成分来解释最大方差。

       

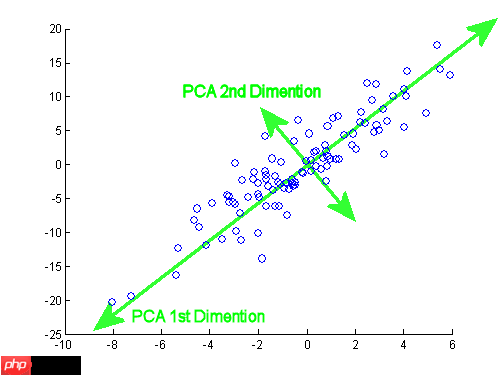
所以对于上面的图像，如果我们把所有的点都投射在PCA一维上，那么这些点比在其他轴上投射更分散。这意味着PCA一维解释了最大的方差，因此它是我们的第一主成分。现在我们考虑垂直于这个分量的分量，由于这个数据是2维的，我们只有1个垂直于1维主成分的分量，它就成为我们的2维主成分。

注意：如果我们有第三维数据从屏幕上出来，那么我们将有2个垂直于第一主成分的成分，我们将不得不选择一个能解释两个主成分的最大方差。

一旦我们有了这些主成分，我们就可以选择我们希望拥有的成分数量，然后用这些主成分来表达我们的数据，从而减少维度。

所以我们在我们的案例中也是这样做的。我们将选择分量的数量，使我们的数据在较低的维度上能解释我们原始数据95%的方差。

In [31]

from sklearn.decomposition import PCApca = PCA(n_components=0.95)X_red = pca.fit_transform(df)

登录后复制    

有了这些，我们就可以做我们一直想做的事情，即聚类。我们将使用Kmeans聚类算法从我们的数据集中额外提取信息集群。

模型培训

了解KMeans聚类算法的实际工作原理是相当有趣和直观的。

KMeans聚类是一种无监督的聚类算法，它将同一聚类中的相似数据聚在一起，形成k个聚类。结果我们得到了相似记录的群组，然后可以对这些记录进行相应的标记和操作。

该算法是如何找到聚类的呢？

给定k个簇的数量，它首先选择k个随机点（可能不是数据集中的点）作为k个簇的中心点。

然后我们将每个点分配给最接近的中心点，形成k个簇。

一旦所有的点都被分配到一个簇中，我们就为每个簇计算新的中心点。

然后我们将点重新分配到最接近的中心点。

如果任何重新分配发生在步骤4，我们重复步骤3和4。如果没有发生重新分配，那么我们的模型已经准备好了，我们已经从我们的数据集中提取了k个聚类。

这个过程将在下图中解释。

       

但有一个问题。由于算法本身是以随机初始化k点开始的，所以很多事情都取决于初始化。由于我们现实世界的数据并不像上图中的数据那样泾渭分明，所以可能会发生这样的情况，即模型初始化k点的方式，我们最终可能会得到一个次优的解决方案。

为了避免这种情况，我们可以在每次迭代时用随机初始点多次运行算法。多次运行模型可以保证至少有一次我们避免了不好的初始化，达到最优解。Scikit learn实际上是对一个KMeans模型进行10次训练，我们可以通过if n_init超参数的帮助来控制。

为了衡量哪种模型在n次随机初始化中表现更好，我们可以使用模型innertia或wcss（Within Cluster Summation of Squares）。它测量的是每个点与其中心点的距离之和。所以我们希望紧凑的簇中的点尽可能的接近它的中心点。

另一种避免不良初始化的方法是使用KMeans++算法来初始化中心点。这个算法初始化中心点的方式是使所选择的中心点尽可能的相互接近，从而确保我们没有次优的解决方案。这个算法与前面的方法一起确保我们获得最佳的解决方案。Scikit learn使用KMeans++算法来初始化中心点，并由init超参数给出。

在这之前的整个讨论都是围绕着我们知道簇数n的假设进行的，因此n是这里最重要的超参数，必须将n初始化到合适的值。

为了得到n的值，我们不能使用innertia作为我们的度量，因为随着簇数的增加，innertia会不断增加。想一想，如果我们将n初始化为数据集中的点的数量，那么innertia将是最小的。

有一种方法可以绘制n与innertia的关系图，当我们绘制这个图时，我们可以发现一个肘部，在这个肘部之后，innertia会以更低的速度下降。如果我们可以用这个肘点对应的n作为我们的簇数。

另一种方法是计算轮廓分，它的计算公式为(b-a)/min(a,b)，其中b->到最近集群实例的平均距离，a->到同一集群其他实例的平均距离。因此，如果到其他簇的点的平均距离减小，而到同一簇的点的平均距离增大，则剪影得分对模型进行惩罚。而如果到其他集群的点的平均距离增加，而到同一集群的点的平均距离减少，则奖励模型。因此我们可以选择一个剪影得分最高的模型。

Phew! 你还在这里？好了，理论够了。让我们在实践中看看这一切。

In [32]

from sklearn.cluster import KMeanskmeans_models = [KMeans(n_clusters=k, random_state=23).fit(X_red) for k in range (1, 10)]innertia = [model.inertia_ for model in kmeans_models]plt.plot(range(1, 10), innertia)plt.title('Elbow method')plt.xlabel('Number of Clusters')plt.ylabel('WCSS')plt.show()

登录后复制        

登录后复制登录后复制                

你看到那里的拐点了吗? 拐点好像是3、4左右 。我们用剪影分来看看哪个表现更好。

In [33]

from sklearn.metrics import silhouette_scoresilhoutte_scores = [silhouette_score(X_red, model.labels_) for model in kmeans_models[1:4]]plt.plot(range(2,5), silhoutte_scores, "bo-")plt.xticks([2, 3, 4])plt.title('Silhoutte scores vs Number of clusters')plt.xlabel('Number of clusters')plt.ylabel('Silhoutte score')plt.show()

登录后复制        

登录后复制登录后复制                

好吧，我们错了n=2似乎比其他两个有更高的轮廓。所以, 我们将选择2作为我们的聚类数量。

模型评估和预测

In [34]

from sklearn.metrics import silhouette_scorekmeans = KMeans(n_clusters=2, random_state=23)kmeans.fit(X_red)print('Silhoutte score of our model is ' + str(silhouette_score(X_red, kmeans.labels_)))

登录后复制        

Silhoutte score of our model is 0.8700455999561426

登录后复制        

将标签作为簇索引分配给我们的数据集。

In [35]

df['cluster_id'] = kmeans.labels_

登录后复制登录后复制    

将我们前面做的对数变换进行逆向变换，将结果在原比例上可视化。

In [36]

for col in cols:    df[col] = np.exp(df[col])

登录后复制    In [37]

plt.figure(figsize=(10,6))sns.scatterplot(data=df, x='ONEOFF_PURCHASES', y='PURCHASES', hue='cluster_id')plt.title('Distribution of clusters based on One off purchases and total purchases')plt.show()

登录后复制登录后复制        

登录后复制登录后复制登录后复制登录后复制                In [38]

plt.figure(figsize=(10,6))sns.scatterplot(data=df, x='CREDIT_LIMIT', y='PURCHASES', hue='cluster_id')plt.title('Distribution of clusters based on Credit limit and total purchases')plt.show()

登录后复制登录后复制        

登录后复制登录后复制登录后复制登录后复制                

看上面2张图，好像我们的模型把信用卡使用率低的客户聚在了一个聚类，而把使用率较高的模型聚在了另一个聚类。很好！我们对资源进行相应的引导。

附带:

3似乎是一个拐点，所以我想知道3聚类的模型是什么样子.

In [39]

kmeans = KMeans(n_clusters=3, random_state=23)kmeans.fit(X_red)

登录后复制        

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,       n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',       random_state=23, tol=0.0001, verbose=0)

登录后复制                In [40]

df['cluster_id'] = kmeans.labels_

登录后复制登录后复制    In [41]

plt.figure(figsize=(10,6))sns.scatterplot(data=df, x='ONEOFF_PURCHASES', y='PURCHASES', hue='cluster_id')plt.title('Distribution of clusters based on One off purchases and total purchases')plt.show()

登录后复制登录后复制        

登录后复制登录后复制登录后复制登录后复制                In [42]

plt.figure(figsize=(10,6))sns.scatterplot(data=df, x='CREDIT_LIMIT', y='PURCHASES', hue='cluster_id')plt.title('Distribution of clusters based on Credit limit and total purchases')plt.show()

登录后复制登录后复制        

登录后复制登录后复制登录后复制登录后复制                

在我看来，这似乎是更好的聚类方法，因为它确实可以将使用信用卡次数多的上半数客户和使用次数少的客户区分开来。如果我们想根据信用卡的使用情况来指导我们的营销策略，这似乎是一个更可操作的结果。