绕不过的BP算法，从这里开始！

本文围绕BP算法展开，先简介其作为双向算法的本质，接着详细呈现初始化神经元、信息前向传播等步骤的代码及批注，还通过解决异或问题和预测小麦品种分类的实例，展示了BP算法的实现与应用，包括网络训练、误差计算等过程。

绕不过的BP算法，从这里开始！

其实对于每个机器学习和深度学习的初学者来说，都绕不开一个算法，那就是bp算法。我参考了张玉宏-《深度学习之美》这本书并编写这篇推文，本文主要是对BP算法的代码实现和详细的批注，希望对你学习有所帮助。阅读之前可以看一下这篇文章学习下基本原理——BP算法双向传，链式求导最缠绵，个人认为已经讲的非常详细易懂了。

再一个推荐一篇文章，或许对你的AI学习生涯有所帮助——李沐：用随机梯度下降来优化人生！

1.BP算法简介

BP 算法，在本质上是一个好用的优化函数 。 说到 BP 算法，我们通常强调的是反向传播 。 其实在本质上，它是一个双向算法。

正向传播输入信号，输出分类信息（对于有监督学习而言，基本上都可归属于分类算法）

反向传播误差信息，调整全网权值（通过微调网络参数，让下一轮的输出更加准确）

2.初始化神经元

定义的网络是只有一个隐含层（ 2 个神经元）和输出层（ 2 个神经元）的神经网络。

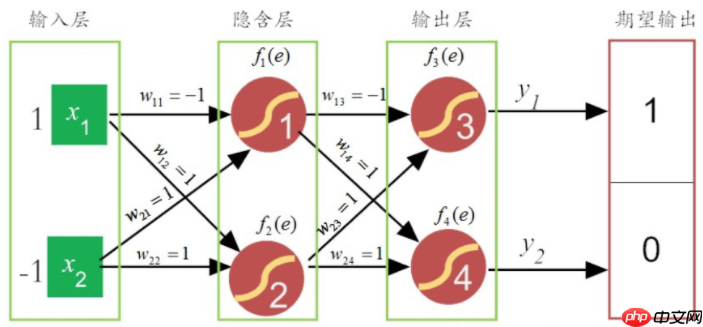
from random import seedfrom random import random# 初始化网络，n_inputs输入神经元数量，n_hidden隐含层神经元的个数，n_outputs输出神经元的个数def initialize_network(n_inputs, n_hidden, n_outputs):    network = list()    # 隐含层，多出一个权值是留给偏置的。    hidden_layer = [{'weights': [random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]    network.append(hidden_layer)    output_layer = [{'weights': [random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]    network.append(output_layer)    return networkif __name__ == '__main__':    seed(1)    network = initialize_network(2, 2, 2)    for layer in network:        print(layer)

3.信息前向传播

信息前向传播，简单说来，就是把信号通过激活函数的加工，一层一层的向前“蔓延”，直到抵达输出层。在这里，假设神经元内部的激活函数为Sigmod（f(x)=1/(1+e−x))Sigmod（f(x)=1/(1+e−x))。之所以选用这个激活函数，主要因为它的求导形式非常简洁而优美：

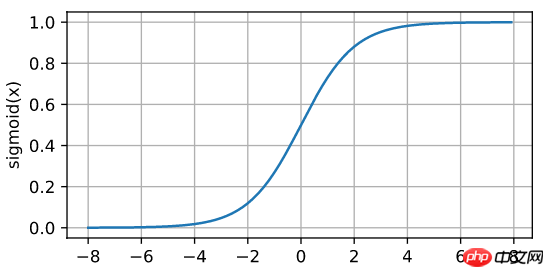
事实上，类似于感知机，每一个神经元的功能都可细分两大部分：

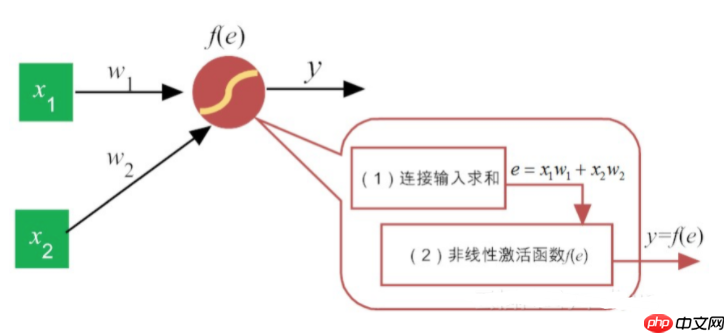
# 计算神经元的激活值（加权之和）def activate(weights, inputs):    activation = weights[-1] # 实际是指weights[-1]*1即偏置乘以1    for i in range(len(weights) - 1):        activation += weights[i] * inputs[i]    return activation

一旦神经元被激活，它的输出取决于激活函数的特性。因此，下面的工作就是设计激活函 数。激活函数有多种，如Sigmoid、Tanh或ReLU等。为简单起见，我们还是选 择传统的Sigmoid，它的定义非常简单。

# 神经元的激活函数def transfer(activation):    return 1.0 / (1.0 + exp(-activation))

4.BP 算法的前向传播

下面，设计一个前向传播函数 forward_propagate（），它把原始数据的每一行作为一个输入，然后计算一次输出 。 我们利用一个数组new_inputs ，记录前一层的输出，然后让其作为下一层新的输入

from math import exp# 计算神经元的激活值（加权之和）def activate(weights, inputs):    activation = weights[-1]  # 实际是指weights[-1]*1    for i in range(len(weights) - 1):        activation += weights[i] * inputs[i]    return activation# 神经元的激活函数def transfer(activation):    return 1.0 / (1.0 + exp(-activation))# 计算神经网络的正向传播def forward_propagate(network, row):    inputs = row    for layer in network:        new_inputs = []        for neuron in layer:            activation = activate(neuron['weights'], inputs)            # 添加新属性直接给出新key赋值就行            neuron['output'] = transfer(activation)            new_inputs.append(neuron['output'])            print(neuron)        inputs = new_inputs    return inputsif __name__ == '__main__':    # 测试正向传播，注意权值是输出层计算两个神经元的权值    network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]},                {'weights': [0.2550690257394217, 0.49543508709194095, 0.4494910647887381]}],               [{'weights': [0.651592972722763, 0.7887233511355132, 0.0938595867742349]},                {'weights': [0.02834747652200631, 0.8357651039198697, 0.43276706790505337]}]]    # 表明这是一个样本，它有两个特征，代表输入层有两个神经元，    # 它们的特征值分别是“ 1 ”和“0”，最后一个值为“None”，表示预期的输出值 。    row = [1, 0, None]    output = forward_propagate(network, row)    print(output)

5.BP 算法的误差反向传播

在计算出网络的正向输出后，下面就该计算误差了。这里的误差是指预期输出（可视为一个常数）和前向传播的实际输出之间的差值。这个差值作为网络权值调控的信号，反向传递给各个隐含层，让其按照预定的规则更新权值。

反向传播过程中要用到传递函数的导数。当我们采用Sigmoid作为激活函数时，它的求导形式是非常简单的，它的求导形式为f′(x)=f(x)(1−f(x))f′(x)=f(x)(1−f(x))即：(11+e−x)′=11+e−x(1−11+e−x)(1+e−x1)′=1+e−x1(1−1+e−x1)，所以直接把激活函数得到的值带入就行。

# 计算激活函数的导数def transfer_derivative(output):    return output * (1.0 - output)

# 反向传播误差信息，并存储在神经元中def backward_propagate_error(network, expected):    # reversed返回一个反转的迭代器，i是从1开始再到0，所以先到输出层    for i in reversed(range(len(network))):        layer = network[i]        errors = list()        if i != len(network)-1:  # 筛选出隐含层            for j in range(len(layer)):                error = 0.0  # 令误差为0                # 计算每个神经元的“加权误差”                for neuron in network[i + 1]:                    error += (neuron['weights'][j] * neuron['responsibility'])                errors.append(error)        else:  # 这个为输出层            for j in range(len(layer)):                neuron = layer[j]                errors.append(expected[j] - neuron['output'])        # 计算隐含层神经元的纠编责任        for j in range(len(layer)):            neuron = layer[j]            # 第一遍先计算出输出层纠偏责任，然后输出层责任，反向传播到隐含层进行加工处理。            # 第二遍计算隐含层神经元的纠偏责任            neuron['responsibility'] = errors[j] * transfer_derivative(neuron['output'])if __name__ == '__main__':    # 测试反向传播，数据为上文中正向输出结果    network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614], 'output': 0.7105668883115941},                {'weights': [0.2550690257394217, 0.49543508709194095, 0.4494910647887381], 'output': 0.6691980263750579}],               [{'weights': [0.651592972722763, 0.7887233511355132, 0.0938595867742349], 'output': 0.7473771139195361},                {'weights': [0.02834747652200631, 0.8357651039198697, 0.43276706790505337], 'output': 0.733450902916955}]]    # 预期的输出值    expected = [0, 1]    backward_propagate_error(network, expected)    for layer in network:        print(layer)

输出：

[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614], 'output': 0.7105668883115941, 'responsibility': -0.01860577502351945}, {'weights': [0.2550690257394217, 0.49543508709194095, 0.4494910647887381], 'output': 0.6691980263750579, 'responsibility': -0.014996444841496356}][{'weights': [0.651592972722763, 0.7887233511355132, 0.0938595867742349], 'output': 0.7473771139195361, 'responsibility': -0.14110820977007524}, {'weights': [0.02834747652200631, 0.8357651039198697, 0.43276706790505337], 'output': 0.733450902916955, 'responsibility': 0.05211052864753572}]

从输出结果可以看出，反向传播后，网络的权值并没有发生变化。这是因为为了简化网络的反向传播过程，我们并没有添加权值更新的操作。

权值的反向传播过程可以另行定义函数update_weights( ）来实现，在后面的训练网络中，我们会使用这个函数，并会给出详细实现。

# 根据误差，更新网络权重def update_weights(network, row, l_rate):    for i in range(len(network)):        inputs = row[:-1]  # 0到倒数第一个，不要最后一个，最后一个为预期值        if i != 0:  # 如果不是输入层,inputs会改变            # 上一层的输出就是这一层的输入            inputs = [neuron['output'] for neuron in network[i - 1]]        for neuron in network[i]:            for j in range(len(inputs)):                # 本身权值加上误差，从而更新                neuron['weights'][j] += l_rate * neuron['responsibility'] * inputs[j]            # 最后一个权值是偏置的权值，则默认输入为1            neuron['weights'][-1] += l_rate * neuron['responsibility']

6.训练网络（解决异或问题）

结合前面的分析，下面我们给出BP算法的全部代码，这里包括权值更新函数update_weights( ）。训练的数据就是“异或”真值表，然后我们用这个训练好的网络，来测试它的正确性。

from math import expfrom random import seedfrom random import random# 初始化神经网络，n_inputs输入神经元数量，n_hidden隐含层神经元的个数，n_outputs输出神经元的个数def initialize_network(n_inputs, n_hidden, n_outputs):    network = list()    # 隐含层，多出一个权值是留给偏置的    hidden_layer = [{'weights': [random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]    network.append(hidden_layer)    output_layer = [{'weights': [random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]    network.append(output_layer)    return network# 计算神经元的激活值（加权之和）def activate(weights, inputs):    activation = weights[-1]    for i in range(len(weights)-1):        activation += weights[i] * inputs[i]    return activation# 定义激活函数def transfer(activation):    return 1.0 / (1.0 + exp(-activation))# 计算神经网络的正向传播，row为输入def forward_propagate(network, row):    inputs = row    for layer in network:        new_inputs = []        for neuron in layer:            activation = activate(neuron['weights'], inputs)            neuron['output'] = transfer(activation)            new_inputs.append(neuron['output'])        inputs = new_inputs  # 更新下一层的输入    return inputs# 计算激活函数的导数def transfer_derivative(output):    return output * (1.0 - output)# 反向传播误差信息，并将纠偏责任存储在神经元中def backward_propagate_error(network, expected):    # reversed返回一个反转的迭代器，i是从1开始再到0，所以先到输出层    for i in reversed(range(len(network))):        layer = network[i]        errors = list()        if i != len(network)-1:  # 隐含层            for j in range(len(layer)):                error = 0.0                for neuron in network[i + 1]:                    error += (neuron['weights'][j] * neuron['responsibility'])                errors.append(error)        else:  # 输出层            for j in range(len(layer)):                neuron = layer[j]                errors.append(expected[j] - neuron['output'])        # 第一遍先计算输出层纠偏责任，第二遍是计算隐含层神经元纠偏责任        for j in range(len(layer)):            neuron = layer[j]            neuron['responsibility'] = errors[j] * transfer_derivative(neuron['output'])# 根据误差，更新网络权重def update_weights(network, row, l_rate):    for i in range(len(network)):        inputs = row[:-1]  # 0到倒数第一个，不要最后一个，最后一个为预期值        if i != 0:  # 如果不是输入层,inputs会改变            # 上一层的输出就是这一层的输入            inputs = [neuron['output'] for neuron in network[i - 1]]        for neuron in network[i]:            for j in range(len(inputs)):                # 本身权值加上误差，从而更新                neuron['weights'][j] += l_rate * neuron['responsibility'] * inputs[j]            # 最后一个权值是偏置的权值，则默认输入为1            neuron['weights'][-1] += l_rate * neuron['responsibility']# 根据指定的训练周期训练网络def train_network(network, train, l_rate, n_epoch, n_outputs):    for epoch in range(n_epoch):        sum_error = 0        for row in train:            outputs = forward_propagate(network, row)            expected = [0 for i in range(n_outputs)]            expected[row[-1]] = 1            sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])            backward_propagate_error(network, expected)            update_weights(network, row, l_rate)        print('>周期=%d, 误差=%.3f' % (epoch, sum_error))def predict(network, row):    outputs = forward_propagate(network, row)    # 找到最大输出的位置    return outputs.index(max(outputs))if __name__ == '__main__':    # 测试BP网络    seed(2)    dataset = [[1, 1, 0],               [1, 0, 1],               [0, 1, 1],               [0, 0, 0]]    n_inputs = len(dataset[0]) - 1    n_outputs = len(set([row[-1] for row in dataset]))    network = initialize_network(n_inputs, 2, n_outputs)    train_network(network, dataset, 0.5, 20000, n_outputs)    for layer in network:        print(layer)    for row in dataset:        prediction = predict(network, row)        print('预期值=%d, 实际输出值=%d' % (row[-1], prediction))

输出：

>周期=19997, 误差=0.001>周期=19998, 误差=0.001>周期=19999, 误差=0.001[{'weights': [7.712477744545061, 7.7440900975746905, -3.5650021384039166], 'output': 0.02751936416589607, 'responsibility': -8.376641916462031e-05}, {'weights': [5.8564929714867615, 5.86347099793969, -8.960096811842467], 'output': 0.00012841729893459846, 'responsibility': 4.229813720805575e-07}][{'weights': [-9.737063526539211, 10.247803365255386, 4.6152795787843885], 'output': 0.987239489131048, 'responsibility': 0.00016075283551528197}, {'weights': [9.737461040040083, -10.24823169595781, -4.615466538222714], 'output': 0.012758292571173627, 'responsibility': -0.00016069731064246199}]预期值=0, 实际输出值=0预期值=1, 实际输出值=1预期值=1, 实际输出值=1预期值=0, 实际输出值=0

7.利用BP算法预测小麦品种的分类

作为有监督学习的算法代表 ，BP 算法有两大用途 ， 一是离散输出用作分类 ， 二是连续输出用作回归 。

有监督学习算法都要用到训练集。这里我们采用的是加州大学埃文分校（UCI）的机器学习数据仓库，该仓库维护了大约300多个机器学习的常用数据集。本次使用的数据集是小麦种子数据。该数据集把小麦种子分为三个品类：Canadian,Kama和Rosa，分别用数字1、2和3表示。评判的依据是小麦种子的7个特征，它们依次是：面积（area,AA）、周长（perimeter, PP）、紧密度（compactness, C=4πA/P2C=4πA/P2）、麦粒核的长度（length of kernel ）、麦粒核的宽度（width of kernel）、偏度系数（asymmetry coefficient）、麦粒槽长度（length of kernel groove）。这个数据集合共有210条数据，下面是从数据集合中随机抽取的6条数据。

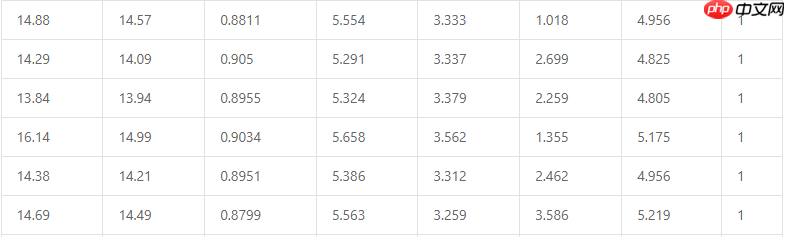
本例中的小麦种子，共有7个特征，所以输入层就设计为7个神经元。因为我们的输出是小麦的三个分类，因此输出层的神经元个数就设定为3。现在主要的工作集中在如何设计合理的隐含层。为简单起见，这里暂时仅设计一个隐含层，该层中的神经元个数为5。这样的设定其实并没有太多的道理可言，更多凭借的是设计者的（调参）经验，它们可被视为一种超参数。

为了验证算法的正确性，我们利用交叉验证的方法，把 210 个数据样本等分为 5 份，训练集和测试集彼此轮流互换，最后计算出的误差分数以其大小作为衡量算法准确性的度量（自然，这个值越小越好）。

"""BP算法在小麦种子分类中的应用"""from random import seedfrom random import randrangefrom random import randomfrom csv import readerfrom math import exp# 数据读取class Database():    def __init__(self, db_file):        self.filename = db_file        self.dataset = list()    # 导入CSV 文件    def load_csv(self):        with open(filename, 'r') as file:            csv_reader = reader(file)            for row in csv_reader:                if not row:  # 判定是否有空行，如有，则跳入到下一行                    continue                self.dataset.append(row)#        print(self.dataset)    # 将n-1列的属性字符串列转换为浮点数，第n列为分类的类别    def dataset_str_to_float(self):        col_len = len(self.dataset[0]) - 1        for row in self.dataset:            for column in range(col_len):                row[column] = float(row[column].strip())    # 将最后一列（n）的类别，转换为整型，并提取有多少个类（最后一列就是实际类型）    def str_column_to_int(self, column):        class_values = [row[column] for row in self.dataset]  # 读取指定列的数字        unique = set(class_values)  # 用集合来合并类        lookup = dict()        for i, value in enumerate(unique):            lookup[value] = i        for row in self.dataset:            row[column] = lookup[row[column]]    # 找到每一列（属性）的最小和最大值    def dataset_minmax(self):        self.minmax = list()        self.minmax = [[min(column), max(column)] for column in zip(*self.dataset)]    # 将数据集合中的每个（列）属性都规整化到0-1    def normalize_dataset(self):        self.dataset_minmax()        for row in self.dataset:            for i in range(len(row)-1):                row[i] = (row[i] - self.minmax[i][0]) / (self.minmax[i][1] - self.minmax[i][0])    def get_dataset(self):        # 构建训练数据        self.load_csv()        self.dataset_str_to_float()        self.str_column_to_int(len(self.dataset[0])-1)        self.normalize_dataset()        return self.dataset# BP网络训练class BP_Network():    # 初始化神经网络    def __init__(self, n_inputs, n_hidden, n_outputs):        self.n_inputs = n_inputs        self.n_hidden = n_hidden        self.n_outputs = n_outputs        self.network = list()        hidden_layer = [{'weights': [random() for i in range(self.n_inputs + 1)]} for i in range(self.n_hidden)]        self.network.append(hidden_layer)        output_layer = [{'weights': [random() for i in range(self.n_hidden + 1)]} for i in range(self.n_outputs)]        self.network.append(output_layer)    # 计算神经元的激活值（加权之和）    def activate(self, weights, inputs):        activation = weights[-1]        for i in range(len(weights)-1):            activation += weights[i] * inputs[i]        return activation    # 定义激活函数    def transfer(self, activation):        return 1.0 / (1.0 + exp(-activation))    # 计算神经网络的正向传播    def forward_propagate(self, row):        inputs = row        for layer in self.network:            new_inputs = []            for neuron in layer:                activation = self.activate(neuron['weights'], inputs)                neuron['output'] = self.transfer(activation)                new_inputs.append(neuron['output'])            inputs = new_inputs        return inputs    # 计算激活函数的导数    def transfer_derivative(self, output):        return output * (1.0 - output)    # 反向传播误差信息，并将纠偏责任存储在神经元中    def backward_propagate_error(self, expected):        for i in reversed(range(len(self.network))):            layer = self.network[i]            errors = list()            if i != len(self.network)-1:                for j in range(len(layer)):                    error = 0.0                    for neuron in self.network[i + 1]:                        error += (neuron['weights'][j] * neuron['responsibility'])                    errors.append(error)            else:                for j in range(len(layer)):                    neuron = layer[j]                    errors.append(expected[j] - neuron['output'])            for j in range(len(layer)):                neuron = layer[j]                neuron['responsibility'] = errors[j] * self.transfer_derivative(neuron['output'])    # 根据误差，更新网络权重    def _update_weights(self, row):        for i in range(len(self.network)):            inputs = row[:-1]            if i != 0:                inputs = [neuron['output'] for neuron in self.network[i - 1]]            for neuron in self.network[i]:                for j in range(len(inputs)):                    neuron['weights'][j] += self.l_rate * neuron['responsibility'] * inputs[j]                neuron['weights'][-1] += self.l_rate * neuron['responsibility']    # 根据指定的训练周期训练网络    def train_network(self, train):        for epoch in range(self.n_epoch):            sum_error = 0            for row in train:                outputs = self.forward_propagate(row)                expected = [0 for i in range(self.n_outputs)]                expected[row[-1]] = 1                sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])                self.backward_propagate_error(expected)                self._update_weights(row)            print('>周期=%d, 误差=%.3f' % (epoch, sum_error))    # 利用训练好的网络，预测“新”数据    def predict(self, row):        outputs = self.forward_propagate(row)        return outputs.index(max(outputs))    # 利用随机梯度递减策略，训练网络    def back_propagation(self, train, test):        self.train_network(train)        predictions = list()        for row in test:            prediction = self.predict(row)            predictions.append(prediction)        return(predictions)    # 将数据库分割为 n_folds等份    def cross_validation_split(self, n_folds):        dataset_split = list()  # 含有划分成n_folds等份的列表的列表        dataset_copy = list(self.dataset)        fold_size = int(len(self.dataset) / n_folds)        for i in range(n_folds):            fold = list()            while len(fold) < fold_size:                # 输出dataset_copy长度内的随机数                index = randrange(len(dataset_copy))                fold.append(dataset_copy.pop(index))            dataset_split.append(fold)        return dataset_split    # 用预测正确百分比来衡量正确率    def accuracy_metric(self, actual, predicted):        correct = 0        for i in range(len(actual)):            if actual[i] == predicted[i]:                correct += 1        return correct / float(len(actual)) * 100.0    # 用每一个交叉分割的块（训练集合，试集合）来评估BP算法    def evaluate_algorithm(self, dataset, n_folds, l_rate, n_epoch):        self.l_rate = l_rate        self.n_epoch = n_epoch        self.dataset = dataset        folds = self.cross_validation_split(n_folds)        scores = list()        for fold in folds:  # 数据一等份一等份来            train_set = list(folds)            train_set.remove(fold)  # 移出这等份            # sum函数的本意是求和，但在一些特殊的场景下，它还可以完成连接可迭代对象的功能 。            # 完成数据的合并            train_set = sum(train_set, [])  # 剩下的几等份合并            test_set = list()            for row in fold:  # 开始的一等份生成测试集合，并把最后的实际结果设置为None                row_copy = list(row)                test_set.append(row_copy)  # 是添加的本身                row_copy[-1] = None  # 改变了本身的最后一个元素            predicted = self.back_propagation(train_set, test_set)  # 通过训练集合训练后的神经网络，再通过测试集合得到预测值            actual = [row[-1] for row in fold]  # 这是真实值            accuracy = self.accuracy_metric(actual, predicted)  # 通过真实值和预测值评估神经网络            scores.append(accuracy)        return scoresif __name__ == '__main__':    # 设置随机种子    seed(2)    # 构建训练数据    filename = 'data/data110290/seeds_dataset.csv'    db = Database(filename)    dataset = db.get_dataset()    # 设置网络初始化参数    n_inputs = len(dataset[0]) - 1    n_hidden = 5    n_outputs = len(set([row[-1] for row in dataset]))    BP = BP_Network(n_inputs, n_hidden, n_outputs)    l_rate = 0.3    n_folds = 5    n_epoch = 500    scores = BP.evaluate_algorithm(dataset, n_folds, l_rate, n_epoch)    print('评估算法正交验证得分: %s' % scores)    print('平均准确率: %.3f%%' % (sum(scores)/float(len(scores))))

输出：

>周期=0, 误差=162.603>周期=1, 误差=110.506>周期=2, 误差=105.255...>周期=498, 误差=2.599>周期=499, 误差=2.598评估算法正交验证得分: [95.23809523809523, 90.47619047619048, 97.61904761904762, 97.61904761904762, 97.61904761904762]平均准确率: 95.714%