从底层实现决策树并分类实战

本文介绍决策树算法及实现。算法以树形结构推理分类，含根节点、内部节点和叶节点，ID3算法用信息熵测纯度，依信息增益选特征。代码构建贷款数据集，实现香农熵计算、数据集划分等功能，递归生成决策树并测试成功，还分析了决策树的优缺点。

1.算法思想

决策树算法采用树形结构，使用层层推理来实现最终的分类

• 根节点：包含样本的全集
• 内部节点：对应特征属性测试
• 叶节点：代表决策的结果

预测时，在树的内部节点处用某一属性值进行判断，根据判断结果决定进入哪个分支节点，直到到达叶节点处，得到分类结果。 这是一种基于 if-then-else 规则的有监督学习算法，决策树的这些规则通过训练得到，而不是人工制定的。 决策树是最简单的机器学习算法，它易于实现，可解释性强，完全符合人类的直观思维，有着广泛的应用。

使用ID3算法递归构建决策树并使用决策树执行分类

ID3算法（ID意思是 Iterative dichotomiser, 迭代二分器） 一般而言，随着划分过程不断进行，我们希望决策树的分支样本尽可能属于同一类别，即节点的“纯度”(purity)越来越高。 在ID3算法中我们使用信息熵（information entropy）衡量纯度（定义如下），熵越小，纯度越高

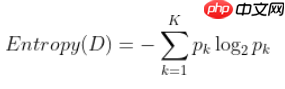
其中，D是样本集，p_k是第k类占比，共有K类 。 ID3算法是以信息增益（information gain）来选择最好的特征的,下面的式子是以属性a作划分的信息增益。

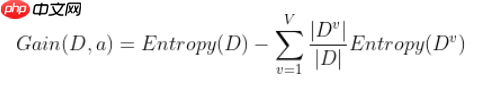
v代表value，指数据集中属性a的取值，我们把不同取值的数据分开，分别计算它们的信息熵，加总即可得到以属性a划分后的信息熵。信息增益对应到决策树上就是父节点信息熵和它的各个子节点信息熵之和的差值。

2.代码实现

2.1数据集制作

• 年龄：0代表青年，1代表中年，2代表老年；
• 有工作：0代表否，1代表是；
• 有自己的房子：0代表否，1代表是；
• 信贷情况：0代表一般，1代表好，2代表非常好；
• 类别(是否给贷款)：0代表否，1代表是。

In [1]

import mathimport collections

In [2]

# 构建数据集def createDataSet():    data_set = [[0, 0, 0, 0, 0],               [0, 0, 0, 1, 0],               [0, 1, 0, 1, 1],               [0, 1, 1, 0, 1],               [0, 0, 0, 0, 0],               [1, 0, 0, 0, 0],               [1, 0, 0, 1, 0],               [1, 1, 1, 1, 1],               [1, 0, 1, 2, 1],               [1, 0, 1, 2, 1],               [2, 0, 1, 2, 1],               [2, 0, 1, 1, 1],               [2, 1, 0, 1, 1],               [2, 1, 0, 2, 1],               [2, 0, 0, 0, 0]]    labels = ['年龄大小', '工作与否', '是否有房', '信贷情况']    return data_set, labelsdata_set,labels=createDataSet()

2.2计算香农熵

统计数据集中的标签

计算标签各自出现的次数

可以借此次数与总标签数，算出一类标签出现的频率，进而算出香农熵

计算所得的香农熵如下

In [3]

# 计算香农熵def entropy(data_set):    n = len(data_set)    labels=[line[-1] for line in data_set]    # print(labels)    labels_dict=collections.Counter(labels)    # print(labels_dict)    entropy = 0    for key in labels_dict:        prob = labels_dict[key] / n        entropy -= prob * math.log2(prob)    return entropyentropy(data_set)

0.9709505944546686

2.3根据指定特征划分数据集

In [4]

# 根据指定特征划分数据集def splitDataSet(data_set, col, value):    reduce_dataset = []    for line in data_set:        if line[col] == value:            line_split=line[:col]+line[col+1:]            reduce_dataset.append(line_split)    return reduce_datasetsplitDataSet(data_set,4,1)

[[0, 1, 0, 1], [0, 1, 1, 0], [1, 1, 1, 1], [1, 0, 1, 2], [1, 0, 1, 2], [2, 0, 1, 2], [2, 0, 1, 1], [2, 1, 0, 1], [2, 1, 0, 2]]

2.4选择最好的特征

随后计算每一个特征的信息增益，并选出最好的特征，流程大致如下

1. 遍历所有特征
2. 使用set去除某一特征的所有取值
3. 根据每一个取值划分原数据集
4. 计算划分后的数据集的信息熵以及划分后数据所占总数据的比例
5. 累加划分后的数据集的信息熵*划分后数据所占总数据的比例，直到遍历完某一特征中的所有取值
6. 计算该特征的信息增益，并取出最高的信息增益，记录下此时的特征

In [5]

# 选择最好的特征def chooseBestFeature(data_set):    num_features = len(data_set[0]) - 1    entropy_dataset = entropy(data_set)    info_gain_end = 0    best_feature = -1    # 遍历所有特征    for i in range(num_features):        # 每个特征中的所有取值        unique_vals = set([example[i] for example in data_set])        new_entropy = 0        for value in unique_vals:            sub_dataSet = splitDataSet(data_set, i, value)            prob = len(sub_dataSet) / len(data_set)            # 条件熵            new_entropy += prob * entropy(sub_dataSet)        info_gain = entropy_dataset - new_entropy                # print(f"第{i}个特征的信息增益为{info_gain:.3f}")        if (info_gain > info_gain_end):            info_gain_end = info_gain            best_feature = i    return best_featurel_num=chooseBestFeature(data_set)print(f'最高的信息增益对应的特征列号为：{l_num}',end='')

最高的信息增益对应的特征列号为：2

In [6]

# 获取label中出现次数最多的标签def majorityCnt(class_list):    class_count = collections.Counter(class_list)    sorted_class_count = sorted(class_count.items(), key = lambda c:c[1], reverse = True)    # print(sorted_class_count)    return sorted_class_count[0][0]majorityCnt([1,1,1,0,0,1,1])

1

2.5递归创建决策树

In [7]

# 递归创建决策树def createTree(data_set, labels, feat_labels):    class_list = [example[-1] for example in data_set]    #类别完全相同停止划分    if class_list.count(class_list[0]) == len(class_list):        return class_list[0]    #遍历到就剩下一个特征时，返回当前最多的lable    if len(data_set[0]) == 1:                                               return majorityCnt(class_list)    #返回最高的信息增益对应的特征列号    best_feat = chooseBestFeature(data_set)    best_featlabel = labels[best_feat]    feat_labels.append(best_featlabel)    #根据最优特征的标签生成树    tree = {best_featlabel:{}}    labels.remove(best_featlabel)    #得到训练集中所有最优特征的属性值    feat_values = [example[best_feat] for example in data_set]    unique_values = set(feat_values)    for value in unique_values:        sub_labels=labels[:]        #遍历最优特征的属性值，使用splitDataSet分割        tree[best_featlabel][value] = createTree(splitDataSet(data_set, best_feat, value), sub_labels, feat_labels)    return tree

2.6使用决策树执行分类

In [8]

# 使用决策树执行分类def classify(input_tree, feat_labels, test_value):    first_str = next(iter(input_tree))    second_dict = input_tree[first_str]    feat_index = feat_labels.index(first_str)    for key in second_dict.keys():        if test_value[feat_index] == key:            if type(second_dict[key]).__name__ == 'dict':                classLabel = classify(second_dict[key], feat_labels, test_value)            else:                classLabel = second_dict[key]    return classLabel

2.7测试

In [9]

# 测试dataSet, labels = createDataSet()featLabels = []tree = createTree(dataSet, labels, featLabels)print(tree)print(featLabels)print(f'测试数据 无房有工作 [0, 1] ->',end=' ')test_value = [0, 1]result = classify(tree, featLabels, test_value)if result == 1:    print('放贷')if result == 0:    print('不放贷')print(f'测试数据 无房无工作 [0, 0] ->',end=' ')test_value = [0, 0]result = classify(tree, featLabels, test_value)if result == 1:    print('放贷')if result == 0:    print('不放贷')print(f'测试数据 有房无工作 [1, 0] ->',end=' ')test_value = [1, 0]result = classify(tree, featLabels, test_value)if result == 1:    print('放贷')if result == 0:    print('不放贷')print(f'测试数据 有房有工作 [1, 1] ->',end=' ')test_value = [1, 1]result = classify(tree, featLabels, test_value)if result == 1:    print('放贷')if result == 0:    print('不放贷')

{'是否有房': {0: {'工作与否': {0: 0, 1: 1}}, 1: 1}}['是否有房', '工作与否']测试数据 无房有工作 [0, 1] -> 放贷测试数据 无房无工作 [0, 0] -> 不放贷测试数据 有房无工作 [1, 0] -> 放贷测试数据 有房有工作 [1, 1] -> 放贷

3.总结

对于构造出的数据产生的决策树

决策树树形结构如下

这里发现其实只有是否有房与工作与否两个选项

• 1代表放贷
• 0代表不放贷

这是因为只需要这两个特征数据，便足以判断出是否要放贷，其余的特征并非重要，故没有作为判断的方式

根据这颗决策树，可以推断出

• 如果有自己的房子 -> 放贷
• 如果没有自己的房子 -> 如果没有工作 -> 不放贷
• 如果没有自己的房子 -> 如果有工作 -> 放贷

构造测试数据 数据如下

• 无房有工作 [0, 1]
• 无房无工作 [0, 0]
• 有房无工作 [1, 0]
• 有房有工作 [1, 1]

将其输入到构建出的决策树中

发现决策树输出的结果符合预期，即决策树构建成功且测试通过

4.决策树的优缺点分析

决策树的优点，如决策树易于理解和解释，可以可视化分析，容易提取出规则，可以同时处理标称型和数值型数据，比较适合处理有缺失属性的样本，测试数据集时，运行速度比较快，在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

决策树的缺点，容易发生过拟合，容易忽略数据集中属性的相互关联，信息增益准则对可取数目较多的属性有所偏好（ID3算法）

In [ ]