【深度学习实战】一、Numpy手撸神经网络实现线性回归

本文围绕用Numpy手撸神经网络实现线性回归展开，先定义包含data和grad的Tensor及初始化类，再实现全连接层、ReLU等层结构，组建模型，还实现带动量的SGD优化器和MSE损失函数，最后以拟合f(x)=sin(x)为例，完成数据处理、模型训练与验证，展示了神经网络底层实现过程。

【深度学习实战】一、Numpy手撸神经网络实现线性回归

一、简介

在学习深度学习时，在理论学习完成后，我们常常会直接使用框架（paddle/torch/tensorflow）来搭建我们的模型，常常忽略了各种层结构的底层实现。学习完成深度学习理论的你，能不能手撸一个简单的模型呢？本文旨在从基础开始，一步一步实现深度学习的参数优化，模型搭建过程，巩固基础知识，从理论到实践，一步一步探索深度学习的奥秘。

本文不会过多介绍深度学习的理论，直接从代码层面来实现全连接层、激活函数和SGD优化器，搭建一个简单的全连接模型，并且以一个线性回归示例，验证模型的效果。

二、目标

本文以学习为目的，以f(x) = sin(x)为目标函数，建立神经网络模型来拟合目标曲线。

数据如下图所示：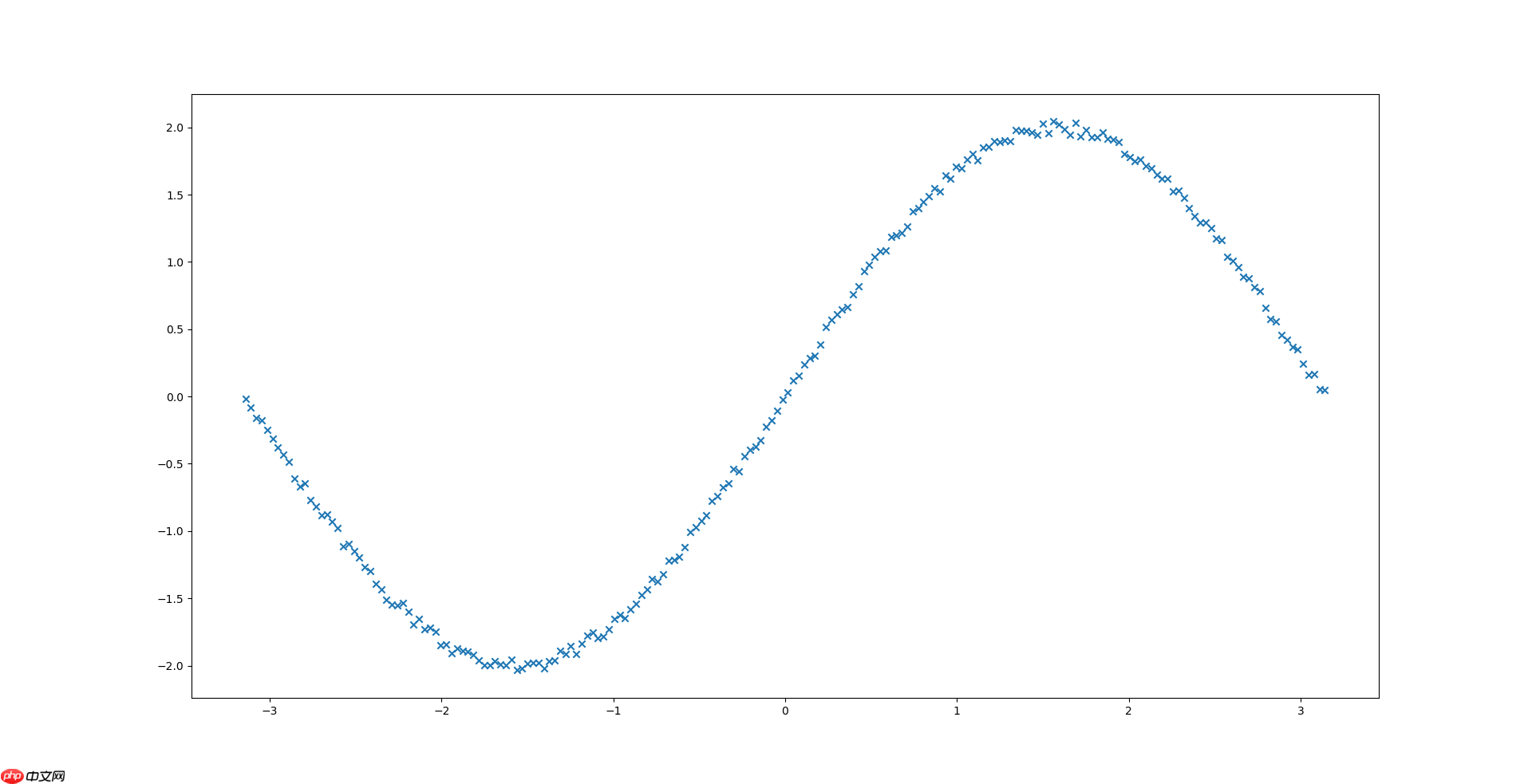        

拟合结果如下图所示：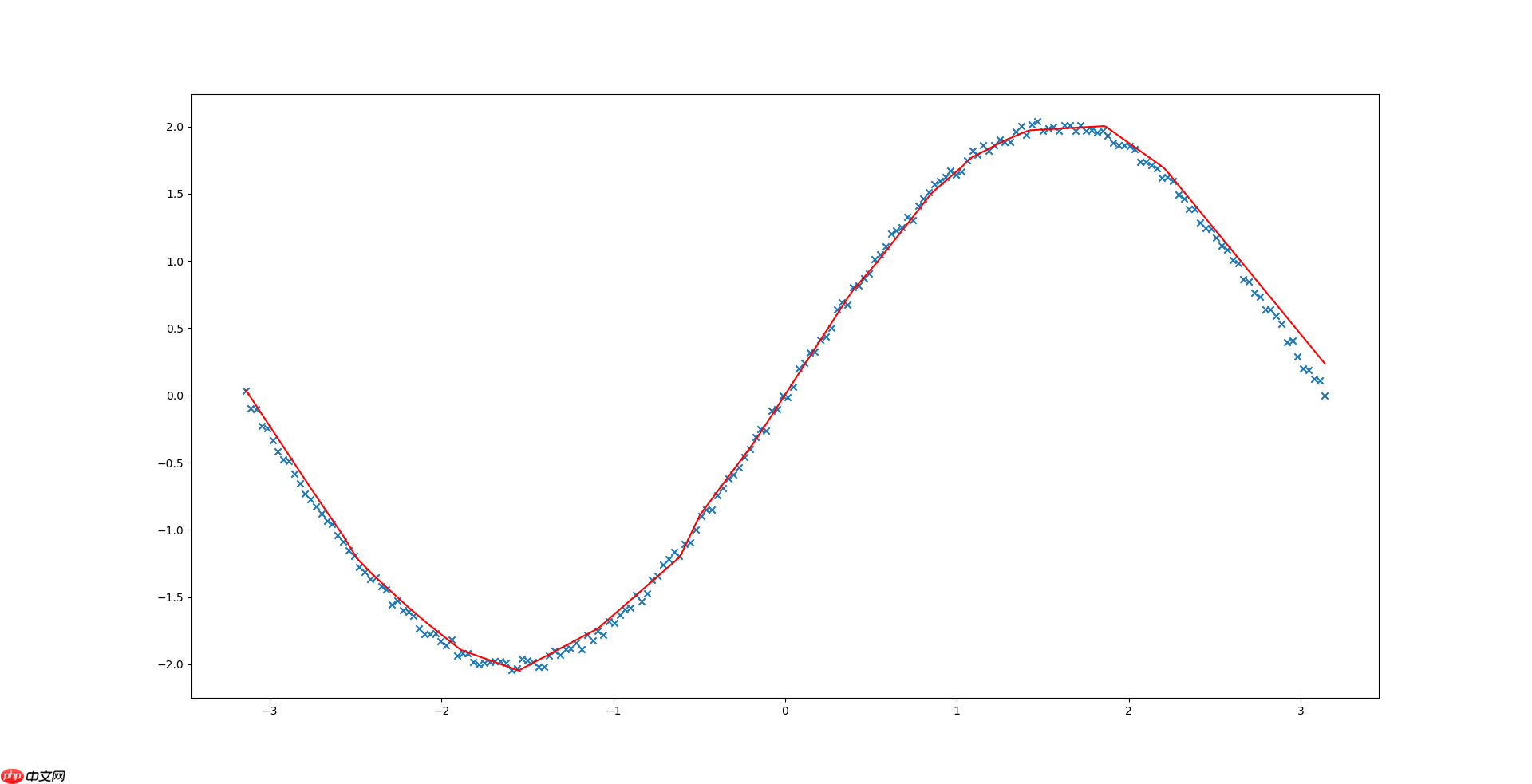        

本文涉及的参考资料：

1、全连接层前向传播和梯度计算
2、动量梯度下降
3、ReLU

三、实现思路

在深度学习框架中，数据都是以tensor的形式进行计算，这里为了简单，数据的输入和输入都是以numpy.ndarray的格式传输。
本小节内容包含了相关类的实现。

1、tensor和初始化

tensor包含data和grad，保存data和对应的梯度数据。

In [1]

# 因为层的参数需要保存值和对应的梯度，这里定义梯度，可训练的参数全部以Tensor的类别保存import numpy as npnp.random.seed(10001)class Tensor:    def __init__(self, shape):        self.data = np.zeros(shape=shape, dtype=np.float32) # 存放数据        self.grad = np.zeros(shape=shape, dtype=np.float32) # 存放梯度    def clear_grad(self):        self.grad = np.zeros_like(self.grad)    def __str__(self):        return "Tensor shape: {}, data: {}".format(self.data.shape, self.data)# Tensor的初始化类，目前仅提供Normal初始化和Constant初始化class Initializer:    """    基类    """    def __init__(self, shape=None, name='initializer'):        self.shape = shape        self.name = name    def __call__(self, *args, **kwargs):        raise NotImplementedError    def __str__(self):        return self.nameclass Constant(Initializer):    def __init__(self, value=0., name='constant initializer', *args, **kwargs):        super().__init__(name=name, *args, **kwargs)        self.value = value    def __call__(self, shape=None, *args, **kwargs):        if shape:            self.shape = shape        assert shape is not None, "the shape of initializer must not be None."        return self.value + np.zeros(shape=self.shape)class Normal(Initializer):    def __init__(self, mean=0., std=0.01, name='normal initializer', *args, **kwargs):        super().__init__(name=name, *args, **kwargs)        self.mean = mean        self.std = std    def __call__(self, shape=None, *args, **kwargs):        if shape:            self.shape = shape        assert shape is not None, "the shape of initializer must not be None."        return np.random.normal(self.mean, self.std, size=self.shape)

登录后复制    

2、Layer

这里实现了全连接层Linear和ReLU激活函数。
1、全连接层前向传播和梯度计算
2、ReLU

In [2]

# 为了使层能够组建起来，实现前向传播和反向传播，首先定义层的基类Layer# Layer的几个主要方法说明：#   forward: 实现前向传播#   backward: 实现反向传播#   parameters: 返回该层的参数，传入优化器进行优化class Layer:    def __init__(self, name='layer', *args, **kwargs):        self.name = name    def forward(self, *args, **kwargs):        raise NotImplementedError    def backward(self):        raise NotImplementedError    def parameters(self):        return []    def __call__(self, *args, **kwargs):        return self.forward(*args, **kwargs)    def __str__(self):        return self.nameclass Linear(Layer):    """    input X, shape: [N, C]    output Y, shape: [N, O]    weight W, shape: [C, O]    bias b, shape: [1, O]    grad dY, shape: [N, O]    forward formula:        Y = X @ W + b   # @表示矩阵乘法    backward formula:        dW = X.T @ dY        db = sum(dY, axis=0)        dX = dY @ W.T    """    def __init__(        self,        in_features,        out_features,        name='linear',        weight_attr=Normal(),        bias_attr=Constant(),        *args,        **kwargs        ):        super().__init__(name=name, *args, **kwargs)        self.weights = Tensor((in_features, out_features))        self.weights.data = weight_attr(self.weights.data.shape)        self.bias = Tensor((1, out_features))        self.bias.data = bias_attr(self.bias.data.shape)        self.input = None    def forward(self, x):        self.input = x        output = np.dot(x, self.weights.data) + self.bias.data        return output    def backward(self, gradient):        self.weights.grad += np.dot(self.input.T, gradient)  # dy / dw        self.bias.grad += np.sum(gradient, axis=0, keepdims=True)  # dy / db         input_grad = np.dot(gradient, self.weights.data.T)  # dy / dx        return input_grad    def parameters(self):        return [self.weights, self.bias]    def __str__(self):        string = "linear layer, weight shape: {}, bias shape: {}".format(self.weights.data.shape, self.bias.data.shape)        return stringclass ReLU(Layer):    """    forward formula:        relu = x if x >= 0             = 0 if x < 0    backwawrd formula:        grad = gradient * (x > 0)    """    def __init__(self, name='relu', *args, **kwargs):        super().__init__(name=name, *args, **kwargs)        self.activated = None    def forward(self, x):        x[x < 0] = 0                     self.activated = x        return self.activated    def backward(self, gradient):        return gradient * (self.activated > 0)

登录后复制    

3、模型组网

将层串联起来，实现前向传播和反向传播。

In [3]

# 模型组网的功能是将层串起来，实现数据的前向传播和梯度的反向传播# 添加层的时候，按照顺序添加层的参数# Sequential方法说明：#   add: 向组网中添加层#   forward: 按照组网构建的层顺序，依次前向传播#   backward: 接收损失函数的梯度，按照层的逆序反向传播class Sequential:    def __init__(self, *args, **kwargs):        self.graphs = []        self._parameters = []        for arg_layer in args:            if isinstance(arg_layer, Layer):                self.graphs.append(arg_layer)                self._parameters += arg_layer.parameters()    def add(self, layer):        assert isinstance(layer, Layer), "The type of added layer must be Layer, but got {}.".format(type(layer))        self.graphs.append(layer)        self._parameters += layer.parameters()    def forward(self, x):        for graph in self.graphs:            x = graph(x)        return x    def backward(self, grad):        # grad backward in inverse order of graph        for graph in self.graphs[::-1]:            grad = graph.backward(grad)    def __call__(self, *args, **kwargs):        return self.forward(*args, **kwargs)    def __str__(self):        string = 'Sequential:\n'        for graph in self.graphs:            string += graph.__str__() + '\n'        return string    def parameters(self):        return self._parameters

登录后复制    

4、优化器

实现了SGD优化器（带动量）
1、动量梯度下降

In [4]

# 优化器主要完成根据梯度来优化参数的任务,其主要参数有学习率和正则化类型和正则化系数# Optimizer主要方法：#   step: 梯度反向传播后调用，该方法根据计算出的梯度，对参数进行优化#   clear_grad: 模型调用backward后，梯度会进行累加，如果已经调用step优化过参数，需要将使用过的梯度清空#   get_decay: 根据不同的正则化方法，计算出正则化惩罚值class Optimizer:    """    optimizer base class.    Args:        parameters (Tensor): parameters to be optimized.        learning_rate (float): learning rate. Default: 0.001.        weight_decay (float): The decay weight of parameters. Defaylt: 0.0.        decay_type (str): The type of regularizer. Default: l2.    """    def __init__(self, parameters, learning_rate=0.001, weight_decay=0.0, decay_type='l2'):        assert decay_type in ['l1', 'l2'], "only support decay_type 'l1' and 'l2', but got {}.".format(decay_type)        self.parameters = parameters        self.learning_rate = learning_rate        self.weight_decay = weight_decay        self.decay_type = decay_type            def step(self):        raise NotImplementedError    def clear_grad(self):        for p in self.parameters:            p.clear_grad()    def get_decay(self, g):        if self.decay_type == 'l1':            return self.weight_decay        elif self.decay_type == 'l2':            return self.weight_decay * g# 基本的梯度下降法为（不带正则化）：# W = W - learn_rate * dW# 带动量的梯度计算方法（减弱的梯度的随机性）：# dW = (momentum * v) + (1 - momentum) * dWclass SGD(Optimizer):    def __init__(self, momentum=0.9, *args, **kwargs):        super().__init__(*args, **kwargs)        self.momentum = momentum        self.velocity = []        for p in self.parameters:            self.velocity.append(np.zeros_like(p.grad))    def step(self):        for p, v in zip(self.parameters, self.velocity):            decay = self.get_decay(p.grad)            v = self.momentum * v + p.grad + decay # 动量计算            p.data = p.data - self.learning_rate * v

登录后复制    

5、损失函数

实现了MSE损失函数。

In [5]

# 损失函数的设计延续了Layer的模式，但是因为需要注意的是forward和backward部分有些不同# MSE_loss = (predict_value - label) ^ 2# MSE方法和Layer的区别：#   forward：y是组网输出的值，target是目标值（这里的输入是组网的输出和目标值），前向传播的同时把dloss / dy 计算出来#   backward: 没有参数，因为在forward的时候，计算出了dloss / dy，所以这里不需要输入参数class MSE(Layer):    """    Mean Square Error:        J = 0.5 * (y - target)^2    gradient formula:        dJ/dy = y - target    """    def __init__(self, name='mse', reduction='mean', *args, **kwargs):        super().__init__(name=name, *args, **kwargs)        assert reduction in ['mean', 'none', 'sum'], "reduction only support 'mean', 'none' and 'sum', but got {}.".format(reduction)        self.reduction = reduction        self.pred = None        self.target = None    def forward(self, y, target):        assert y.shape == target.shape, "The shape of y and target is not same, y shape = {} but target shape = {}".format(y.shape, target.shape)        self.pred = y        self.target = target        loss = 0.5 * np.square(y - target)        if self.reduction is 'mean':            return loss.mean()        elif self.reduction is 'none':            return loss        else:            return loss.sum()    def backward(self):        gradient = self.pred - self.target        return gradient

登录后复制    

6、dataset

In [6]

# 这里仿照PaddlePaddle，Dataset需要实现__getitem__和__len__方法class Dataset:    def __init__(self, *args, **kwargs):        pass    def __getitem__(self, idx):        raise NotImplementedError("'{}' not implement in class {}"                                  .format('__getitem__', self.__class__.__name__))    def __len__(self):        raise NotImplementedError("'{}' not implement in class {}"                                  .format('__len__', self.__class__.__name__))# 根据dataset和一些设置，生成每个batch在dataset中的索引class BatchSampler:    def __init__(self, dataset=None, shuffle=False, batch_size=1, drop_last=False):        self.batch_size = batch_size        self.drop_last = drop_last        self.shuffle = shuffle        self.num_data = len(dataset)        if self.drop_last or (self.num_data % batch_size == 0):            self.num_samples = self.num_data // batch_size        else:            self.num_samples = self.num_data // batch_size + 1        indices = np.arange(self.num_data)        if shuffle:            np.random.shuffle(indices)        if drop_last:            indices = indices[:self.num_samples * batch_size]        self.indices = indices    def __len__(self):        return self.num_samples    def __iter__(self):        batch_indices = []        for i in range(self.num_samples):            if (i + 1) * self.batch_size <= self.num_data:                for idx in range(i * self.batch_size, (i + 1) * self.batch_size):                    batch_indices.append(self.indices[idx])                yield batch_indices                batch_indices = []            else:                for idx in range(i * self.batch_size, self.num_data):                    batch_indices.append(self.indices[idx])        if not self.drop_last and len(batch_indices) > 0:            yield batch_indices# 根据sampler生成的索引，从dataset中取数据，并组合成一个batchclass DataLoader:    def __init__(self, dataset, sampler=BatchSampler, shuffle=False, batch_size=1, drop_last=False):        self.dataset = dataset        self.sampler = sampler(dataset, shuffle, batch_size, drop_last)    def __len__(self):        return len(self.sampler)    def __call__(self):        self.__iter__()    def __iter__(self):        for sample_indices in self.sampler:            data_list = []            label_list = []            for indice in sample_indices:                data, label = self.dataset[indice]                data_list.append(data)                label_list.append(label)            yield np.stack(data_list, axis=0), np.stack(label_list, axis=0)

登录后复制    

四、线性回归示例

本小节的目标是使用上面完成的类，搭建一个简单的模型，并且实现线性拟合的过程。

1、提取数据

In [7]

# 提取训练数据（这里是一个预先生成的f(x) = sin(x) + noise的数据）!unzip -oq ~/data/data119921/sin_data.zip

登录后复制    

2、查看数据分布

In [8]

# 绘制原始数据图像import matplotlib.pyplot as plt%matplotlib inlinex_path = "x.npy"y_path = "y.npy"X = np.load(x_path)Y = np.load(y_path)plt.scatter(X, Y)

登录后复制        

登录后复制                

登录后复制登录后复制登录后复制                

3、搭建模型，设置超参数

In [9]

epoches = 1000batch_size = 4learning_rate = 0.01weight_decay = 0.0train_number = 100 # 选择的训练数据数量，总共200，这里仅挑选一部分训练，否则数据太多过拟合看不出来# 继承之前定义的Dataset，定义一个简单的Datasetclass LinearDataset(Dataset):    def __init__(self, X, Y):        self.X = X        self.Y = Y    def __len__(self):        return len(self.X)    def __getitem__(self, idx):        return self.X[idx], self.Y[idx]# 搭建一个简单的模型model = Sequential(    Linear(1, 16, name='linear1'),    ReLU(name='relu1'),    Linear(16, 64, name='linear2'),    ReLU(name='relu2'),    Linear(64, 16, name='linear2'),    ReLU(name='relu3'),    Linear(16, 1, name='linear2'),)opt = SGD(parameters=model.parameters(), learning_rate=learning_rate, weight_decay=weight_decay, decay_type='l2')loss_fn = MSE()print(model)

登录后复制        

Sequential:linear layer, weight shape: (1, 16), bias shape: (1, 16)relu1linear layer, weight shape: (16, 64), bias shape: (1, 64)relu2linear layer, weight shape: (64, 16), bias shape: (1, 16)relu3linear layer, weight shape: (16, 1), bias shape: (1, 1)

登录后复制        

4、训练

In [10]

# 挑选部分数据训练，数据分布图绘制indexes = np.arange(X.shape[0])train_indexes = np.random.choice(indexes, train_number)X = X[train_indexes]Y = Y[train_indexes]plt.scatter(X, Y)

登录后复制        

登录后复制                

登录后复制登录后复制登录后复制                In [ ]

# 构建dataset和dataloader，开始训练train_dataset = LinearDataset(X, Y)train_dataloader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size, drop_last=True)for epoch in range(1, epoches):    losses = []    for x, y in train_dataloader:        pred = model(x)        loss = loss_fn(pred, y)        losses.append(loss)        grad = loss_fn.backward()        model.backward(grad)        opt.step()        opt.clear_grad()    print("epoch: {}. loss: {}".format(epoch, np.array(losses).mean()))

登录后复制    

5、验证效果

In [12]

# 训练结束，生成比较密集的点，绘制曲线查看模型效果val_number = 500  # 验证点的个数X_val = np.linspace(-np.pi, np.pi, val_number).reshape(val_number, 1)Y_val = np.sin(X_val) * 2val_dataset = LinearDataset(X_val, Y_val)val_dataloader = DataLoader(val_dataset, shuffle=False, batch_size=2, drop_last=False)all_pred = []for x, y in val_dataloader:    pred = model(x)    all_pred.append(pred)all_pred = np.vstack(all_pred)plt.plot(X_val, Y_val, color='green', label='true')plt.plot(X_val, all_pred, color='red', label='predict')plt.legend()plt.show()

登录后复制        

登录后复制登录后复制登录后复制                In [13]

# 打印模型权重for g in model.graphs:    try:        print(g.name, "  weights: ", g.weights.data)        print(g.name, "  bias: ", g.bias.data)    except:        # relu 没有参数        pass

登录后复制        

linear1   weights:  [[-3.39505853e-01  1.82815127e-01  3.41670755e-04  4.51586227e-01   1.53022752e-01  4.51654343e-01 -3.72304150e-01  2.76332489e-01  -1.38630030e-01 -9.45745032e-02 -2.80274033e-02  3.21501804e-01   5.63259058e-04  3.02464553e-01  4.12779030e-01 -5.02756806e-01]]linear1   bias:  [[-0.27559667  0.25060406 -0.00106264  0.25735576  0.15667835 -0.29261948  -0.22068097  0.34773508 -0.06852324 -0.06383495 -0.00121021 -0.20815822  -0.00207523  0.41023867 -0.14955467 -0.27659916]]linear2   weights:  [[ 0.00802045 -0.01371165 -0.02685921 ...  0.02362987 -0.00621883  -0.02786108] [-0.00452856 -0.00503155  0.04844489 ... -0.00561967  0.0025664   0.00678349] [-0.00615242 -0.00192324  0.00115901 ... -0.00903875  0.00314179  -0.01176954] ... [-0.00625044 -0.00103386  0.12367338 ... -0.0048607  -0.01353281  -0.00611369] [ 0.00415564 -0.01963549  0.12541482 ...  0.01609308 -0.00733272  -0.01286687] [ 0.03625054 -0.03395289  0.00589992 ...  0.02610544  0.00226727  -0.01638553]]linear2   bias:  [[-5.80917490e-02  5.01950195e-02 -2.29461260e-01  8.53813886e-01   0.00000000e+00  5.57391247e-03  0.00000000e+00 -1.83248948e-01   2.48837634e-01 -1.11183245e-01 -3.48240873e-01 -4.50779643e-02  -1.28934035e-02  1.12025269e-01  3.79346683e-01  1.35687659e-01   1.21481402e-01 -8.63197975e-02  1.85562909e-03 -2.77419326e-01   7.55994579e-01  0.00000000e+00  0.00000000e+00 -1.42549552e-01   2.88624148e-01 -1.72867527e-01  1.70860914e-01  2.40404679e-01  -8.84156448e-02 -8.03972453e-02 -2.88965818e-01  9.83171145e-02   0.00000000e+00  3.17059611e-01 -1.04739710e-01 -1.16109983e-03   4.49676180e-01  5.43205541e-01  0.00000000e+00  2.16567560e-01   2.66316055e-01  6.52556933e-02  4.21085572e-01 -1.75897451e-01   1.70725040e-01  4.57763929e-01  5.90660615e-02  0.00000000e+00   2.24770074e-01  4.92650106e-01  3.92872747e-01 -1.09088249e-03   3.87059634e-01  1.32970903e-01 -8.24098597e-04  6.95018101e-01  -2.67006851e-01 -3.10753157e-03  0.00000000e+00 -4.12923279e-02  -1.75980184e-02 -4.42488935e-02  0.00000000e+00  4.16345087e-02]]linear2   weights:  [[-0.00030464 -0.01316401 -0.00232969 ... -0.00735164  0.02166657   0.00125336] [ 0.01472182 -0.01163708  0.00238465 ... -0.01319246  0.02852089   0.00038934] [-0.01692646 -0.00244135 -0.00771588 ...  0.05227914 -0.14514223   0.01070569] ... [ 0.00063122  0.00322329 -0.00613279 ... -0.00629652  0.02223584  -0.00575858] [ 0.00141447  0.00212887 -0.01180259 ... -0.00223564  0.00415438   0.00539367] [-0.00545804 -0.01563078  0.00269196 ... -0.01580513  0.0176982  -0.00294621]]linear2   bias:  [[ 2.24308947e-02  4.52850508e-02 -6.85257176e-04  4.71155020e-01  -2.25538467e-02  4.94627319e-01 -3.26158083e-04  8.32043208e-01   1.27510619e+00 -1.93002987e-02  8.65411471e-01 -1.87107957e-02  -2.39317258e-02  3.22988423e-02  8.12310457e-01  1.43143661e-02]]linear2   weights:  [[-0.02986098] [-0.07522691] [-0.00509935] [-0.79988172] [-0.1247629 ] [-0.83384197] [ 0.0070327 ] [ 0.916285  ] [ 1.40066481] [ 0.02468298] [-1.16986177] [-0.17584702] [-0.22990252] [-0.18561223] [ 0.89437478] [-0.02239539]]linear2   bias:  [[0.47546356]]

登录后复制