Gomoku游戏比围棋或象棋简单得多，因此我们可以专注于AlphaZero的训练，在一台PC机上几个小时内就可以获得一个让你不可大意的AI模型——因为一不留心，AI就可能战胜了你。

用飞桨框架2.0造一个会下五子棋的AI模型——从小白到高手的训练之旅

还记得令职业棋手都闻风丧胆的“阿尔法狗”么？这里有“阿尔法狗”的小兄弟——AlphaZero-Gomoku-PaddlePaddle，即我用飞桨框架2.0从零开始训练自己的AI模型，开启五子棋小游戏。

免费影视、动漫、音乐、游戏、小说资源长期稳定更新！ 👉 点此立即查看 👈

       

五子棋游戏简介

五子棋是一种两人对弈的纯策略型棋类游戏，通常双方分别使用黑白两色的棋子，轮流下在棋盘竖线与横线的交叉点上，先形成五子连线者获胜。五子棋容易上手，老少皆宜，而且趣味横生，引人入胜。

本项目简介

本项目是AlphaZero算法的一个实现（使用PaddlePaddle框架），用于玩简单的棋盘游戏Gomoku（也称为五子棋），使用纯粹的自我博弈的方式开始训练。Gomoku游戏比围棋或象棋简单得多，因此我们可以专注于AlphaZero的训练，在一台PC机上几个小时内就可以获得一个让你不可忽视的AI模型——因为一不留心，AI就可能战胜了你。因为和围棋相比，五子棋的规则较为简单，落子空间也比较小，因此没有用到AlphaGo Zero中大量使用的残差网络，只使用了卷积层和全连接层，也正是因为网络结构简单，所以用AIstudio的cpu环境也可以运行（建议使用GPU环境，程序会自动检测环境是否包含GPU，无需手动设置）；本项目之前是用Paddle1.84版本写的，现在升级到paddle2.0版本。AlphaZero是MuZero的“前辈”，了解AlphaZero有助于理解MuZero算法的来龙去脉。开始训练自己的AI模型，请运行“python train.py”；开始人机对战或者AI互搏，请运行“python human_play.py”，15x15棋盘左上角9x9范围下棋的效果展示：

       

让我们用飞桨框架2.0打造一个会下五子棋的AI模型

首先，让我们开始定义策略价值网络的结构，网络比较简单，由公共网络层、行动策略网络层和状态价值网络层构成。在定义好策略和价值网络的基础上，接下来实现PolicyValueNet类，该类主要定义：policy_value_fn()方法，主要用于蒙特卡洛树搜索时评估叶子节点对应局面评分、该局所有可行动作及对应概率，后面会详细介绍蒙特卡洛树搜索；另一个方法train_step()，主要用于更新自我对弈收集数据上策略价值网络的参数。在训练神经网络阶段，我们使用自我对战学习阶段得到的样本集合(s,π,z),训练我们神经网络的模型参数。训练的目的是对于每个输入s, 神经网络输出的p,v和我们训练样本中的π,z差距尽可能的少。损失函数由三部分组成，第一部分是均方误差损失函数，用于评估神经网络预测的胜负结果和真实结果之间的差异。第二部分是交叉熵损失函数，用于评估神经网络的输出策略和我们MCTS输出的策略的差异。第三部分是L2正则化项。In [ ]

%%writefile AlphaZero_Gomoku_PaddlePaddle/policy_value_net_paddlepaddle.pyimport paddleimport numpy as npimport paddle.nn as nn import paddle.nn.functional as Fclass Net(paddle.nn.Layer):    def __init__(self,board_width, board_height):        super(Net, self).__init__()        self.board_width = board_width        self.board_height = board_height        # 公共网络层        self.conv1 = nn.Conv2D(in_channels=4,out_channels=32,kernel_size=3,padding=1)        self.conv2 = nn.Conv2D(in_channels=32,out_channels=64,kernel_size=3,padding=1)        self.conv3 = nn.Conv2D(in_channels=64,out_channels=128,kernel_size=3,padding=1)        # 行动策略网络层        self.act_conv1 = nn.Conv2D(in_channels=128,out_channels=4,kernel_size=1,padding=0)        self.act_fc1 = nn.Linear(4*self.board_width*self.board_height,                                 self.board_width*self.board_height)        self.val_conv1 = nn.Conv2D(in_channels=128,out_channels=2,kernel_size=1,padding=0)        self.val_fc1 = nn.Linear(2*self.board_width*self.board_height, 64)        self.val_fc2 = nn.Linear(64, 1)    def forward(self, inputs):        # 公共网络层         x = F.relu(self.conv1(inputs))        x = F.relu(self.conv2(x))        x = F.relu(self.conv3(x))        # 行动策略网络层        x_act = F.relu(self.act_conv1(x))        x_act = paddle.reshape(                x_act, [-1, 4 * self.board_height * self.board_width])                x_act  = F.log_softmax(self.act_fc1(x_act))                # 状态价值网络层        x_val  = F.relu(self.val_conv1(x))        x_val = paddle.reshape(                x_val, [-1, 2 * self.board_height * self.board_width])        x_val = F.relu(self.val_fc1(x_val))        x_val = F.tanh(self.val_fc2(x_val))        return x_act,x_valclass PolicyValueNet():    """策略&值网络 """    def __init__(self, board_width, board_height,                 model_file=None, use_gpu=True):        self.use_gpu = use_gpu        self.board_width = board_width        self.board_height = board_height        self.l2_const = 1e-3  # coef of l2 penalty                self.policy_value_net = Net(self.board_width, self.board_height)                        self.optimizer  = paddle.optimizer.Adam(learning_rate=0.02,                                parameters=self.policy_value_net.parameters(), weight_decay=self.l2_const)                                             if model_file:            net_params = paddle.load(model_file)            self.policy_value_net.set_state_dict(net_params)                def policy_value(self, state_batch):        """        input: a batch of states        output: a batch of action probabilities and state values        """        # state_batch = paddle.to_tensor(np.ndarray(state_batch))        state_batch = paddle.to_tensor(state_batch)        log_act_probs, value = self.policy_value_net(state_batch)        act_probs = np.exp(log_act_probs.numpy())        return act_probs, value.numpy()    def policy_value_fn(self, board):        """        input: board        output: a list of (action, probability) tuples for each available        action and the score of the board state        """        legal_positions = board.availables        current_state = np.ascontiguousarray(board.current_state().reshape(                -1, 4, self.board_width, self.board_height)).astype("float32")                # print(current_state.shape)        current_state = paddle.to_tensor(current_state)        log_act_probs, value = self.policy_value_net(current_state)        act_probs = np.exp(log_act_probs.numpy().flatten())                act_probs = zip(legal_positions, act_probs[legal_positions])        # value = value.numpy()        return act_probs, value.numpy()    def train_step(self, state_batch, mcts_probs, winner_batch, lr=0.002):        """perform a training step"""        # wrap in Variable        state_batch = paddle.to_tensor(state_batch)        mcts_probs = paddle.to_tensor(mcts_probs)        winner_batch = paddle.to_tensor(winner_batch)        # zero the parameter gradients        self.optimizer.clear_gradients()        # set learning rate        self.optimizer.set_lr(lr)                                             # forward        log_act_probs, value = self.policy_value_net(state_batch)        # define the loss = (z - v)^2 - pi^T * log(p) + c||theta||^2        # Note: the L2 penalty is incorporated in optimizer        value = paddle.reshape(x=value, shape=[-1])        value_loss = F.mse_loss(input=value, label=winner_batch)        policy_loss = -paddle.mean(paddle.sum(mcts_probs*log_act_probs, axis=1))        loss = value_loss + policy_loss        # backward and optimize        loss.backward()        self.optimizer.minimize(loss)        # calc policy entropy, for monitoring only        entropy = -paddle.mean(                paddle.sum(paddle.exp(log_act_probs) * log_act_probs, axis=1)                )        return loss.numpy(), entropy.numpy()[0]        def get_policy_param(self):        net_params = self.policy_value_net.state_dict()        return net_params    def save_model(self, model_file):        """ save model params to file """        net_params = self.get_policy_param()  # get model params        paddle.save(net_params, model_file)

登录后复制        

Overwriting AlphaZero_Gomoku_PaddlePaddle/policy_value_net_paddlepaddle.py

登录后复制        

为什么用MCTS?

在棋盘游戏中（现实生活中也是），玩家在决定下一步怎么走的时候往往会“多想几步”。AlphaGoZero也一样。我们用神经网络来选择最佳的下一步走法后，其余低概率的位置就被忽略掉了。像Minimax这一类传统的AI博弈树搜索算法效率都很低，因为这些算法在做出最终选择前需要穷尽每一种走法。即使是带有较少分支因子的游戏也会使其博弈搜索空间变得像是脱缰的野马似的难以驾驭。分支因子就是所有可能的走法的数量。这个数量会随着游戏的进行不断变化。因此，你可以试着计算一个平均分支因子数，国际象棋的平均分支因子是35，而围棋则是250。这意味着，在国际象棋中，仅走两步就有1,225（35²）种可能的棋面，而在围棋中，这个数字会变成62,500（250²）。现在，时代变了，神经网络将指导并告诉我们哪些博弈路径值得探索，从而避免被许多无用的搜索路径所淹没。接着，蒙特卡洛树搜索算法就将登场啦！

棋类游戏的蒙特卡洛树搜索（MCTS）

使用MCTS的具体做法是这样的，给定一个棋面，MCTS共进行N次模拟。主要的搜索阶段有4个：选择，扩展，仿真和回溯

       

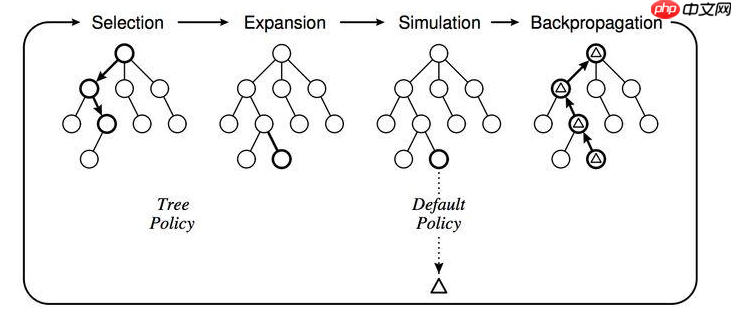
第一步是选择(Selection):这一步会从根节点开始，每次都选一个“最值得搜索的子节点”，一般使用UCT选择分数最高的节点，直到来到一个“存在未扩展的子节点”的节点

第二步是扩展(Expansion)，在这个搜索到的存在未扩展的子节点，加上一个没有历史记录的子节点，初始化子节点

第三步是仿真(simulation)，从上面这个没有试过的着法开始，用一个简单策略比如快速走子策略（Rollout policy）走到底，得到一个胜负结果。快速走子策略一般适合选择走子很快可能不是很精确的策略。因为如果这个策略走得慢，结果虽然会更准确，但由于耗时多了，在单位时间内的模拟次数就少了，所以不一定会棋力更强，有可能会更弱。这也是为什么我们一般只模拟一次，因为如果模拟多次，虽然更准确，但更慢。

第四步是回溯(backpropagation), 将我们最后得到的胜负结果回溯加到MCTS树结构上。注意除了之前的MCTS树要回溯外，新加入的节点也要加上一次胜负历史记录。

相关攻略

热门推荐