当前位置: 首页 > AI > 文章内容页

那些需要守护的

纸嫁衣4红丝缠

蚊子模拟器2022

寿司制作模拟器

鸡尾酒王子

修仙之百世归来

闹鬼的屋子

建造和生存工艺

大王为何独宠我手机

天天快送

【AI达人特训营】高可信度航班延误预测模型及模型可解释性

时间:2025-07-20 作者:游乐小编

随着航空运输市场需求量的不断增加，在规模较大的机场，航班易出现延误。在发生大面积航班延误时，如果没有良好的应对机制，不仅会产生旅客群体性事件，还将带来一系列延误造成的连锁反应。

【ai达人特训营】高可信度航班延误预测模型及模型可解释性 - 游乐网

高可信度航班延误预测模型及模型可解释性

【AI达人特训营】高可信度航班延误预测模型及模型可解释性 - 游乐网

随着航空运输市场需求量的不断增加，在规模较大的机场，航班易出现延误。在发生大面积航班延误时，如果没有良好的应对机制，不仅会产生旅客群体性事件，还将带来一系列延误造成的连锁反应。

本项目基于航班起飞时可以测量的特征，构建MLP模型，以预测航班是否延误。并计算不同特征的重要程度来对模型做出解释，并推断延迟的原因。我们还将使用bootstrapping来估计模型的预测区间。我们利用这些预测区间来建立一种新的模型:在不自信的情况下避免做出预测的模型。该项目所用数据集为2015 Flight Delays and Cancellations数据集的一部分。

关于延误，FAA和BTS将晚点15分钟或以上的航班定义为延误，因此本项目为二分类任务(正点/延误)。

In [1]

!pip install -qq scikit-lego

登录后复制In [138]

# importsimport sysimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.utils import resample #bootstrapfrom sklearn.metrics import accuracy_scorefrom sklearn.preprocessing import StandardScalerfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionfrom sklearn.inspection import permutation_importancefrom sklego.preprocessing import RepeatingBasisFunction #RBFimport paddleimport paddle.nn as nnimport warningswarnings.filterwarnings("ignore",category=DeprecationWarning)

登录后复制In [3]

# 不知道为什么，切换成GPU各种错误，直接CPU得了# https://blog.csdn.net/qq_37668436/article/details/114336142# 最好是V100 32G或以上，CPU核心多paddle.device.set_device("cpu")print(paddle.device.get_device())

登录后复制

cpu

登录后复制

1. Data

该文件原始形状为（10000，10），本节对数据预处理，并构建适合训练的数据形式。

1.1. Preprocessing

如上文所说，首先需要根据ARRIVAL_DELAY来新建DELAY_OR_NOT列，作为真实标签。接着对非数值的分类变量进行独热码操作，如果有缺失值，处理缺失值，扩展数据，并将数据分割为训练集和测试集(8000/2000)。

其中对于时间的编码，可以有些特殊操作：

时间信息的三种编码方式（RBF）https://scikit-lego.netlify.app/preprocessing.html?highlight=repeatingbasisfunctionhttps://scikit-lego.netlify.app/api/preprocessing.html?highlight=repeatingbasisfunction#sklego.preprocessing.RepeatingBasisFunction.fit

使用RBF(radial basis function)对星期和月份编码，可以提升2%左右的准确率。但其中的操作会影响后面的部分，且本文重点不在于性能，因此本次未使用(代码已给出)。

In [4]

# Load the datadf = pd.read_csv('data/data155027/flights.csv')# Create a variable DELAY_OR_NOT that denotes whether ARRIVAL_DELAY is greater than or equal to 15 minutesdf['DELAY_OR_NOT'] = df['ARRIVAL_DELAY'].apply(lambda x: 1 if x >= 15 else 0)df = df.drop(['ARRIVAL_DELAY'], axis=1)df.head()

登录后复制

   DISTANCE  SCHEDULED_TIME  MONTH  SCHED_DEP_HOUR  SCHED_ARR_HOUR  \0      2586             342      9               7              15   1      1235             185      5               6              11   2       184              76      4              17              18   3       862             148      7              19              21   4       236              71      3              20              21      FLIGHT_COUNT  DAY_OF_WEEK ORIGIN_AIRPORT DESTINATION_AIRPORT  DELAY_OR_NOT  0           240            3            SFO                 JFK             1  1           366            4            LAX                 DFW             0  2           172            7            BOS                 LGA             0  3           260            7            IAH                 DEN             1  4           266            2            LAS                 LAX             1

登录后复制In [5]

# # radial basis functions# rbf_weeks = RepeatingBasisFunction(n_periods=7,#                                     remainder='drop',#                                     column='DAY_OF_WEEK',#                                     input_range=(1,7))# rbf_months = RepeatingBasisFunction(n_periods=12, #                                     remainder='drop', #                                     column='MONTH', #                                     input_range=(1,12))        # rbf_weeks.fit(df)# rbf_months.fit(df)# rbfW = rbf_weeks.transform(df)# rbfM = rbf_months.transform(df)

登录后复制In [6]

# use mean values to fill NANdf = df.fillna(df.mean())# one-hot-encode and make certain to drop one column for each predictordf = pd.get_dummies(df, drop_first=True)# # for RBF# X = df.drop(['DELAY_OR_NOT','DAY_OF_WEEK','MONTH'], axis=1)# X = np.concatenate((X, rbfW, rbfM), axis=1)# Split the data into training and test setsX = df.drop(['DELAY_OR_NOT'], axis=1)y = df['DELAY_OR_NOT']X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=111)# scale the datascaler = StandardScaler()X_train = scaler.fit_transform(X_train)X_test = scaler.transform(X_test)# shape of the datasetprint(f'The shape of the X_train is {X_train.shape}')print(f'The shape of the y_train is {y_train.shape}')print(f'The shape of the X_test is {X_test.shape}')print(f'The shape of the y_test is {y_test.shape}')

登录后复制

The shape of the X_train is (8000, 808)The shape of the y_train is (8000,)The shape of the X_test is (2000, 808)The shape of the y_test is (2000,)

登录后复制

1.2. Generate Dataset

定义Dataset来适配该数据集，接着使用DataLoader将数据集化成batch。

In [14]

class FlightDataset(paddle.io.Dataset):    """    步骤一：继承paddle.io.Dataset类    """    def __init__(self, data, label):        """        步骤二：传入data和label        """        super(FlightDataset, self).__init__()        self.num_samples = data.shape[0]        self.data = data        self.label = label    def __getitem__(self, index):        """        步骤三：实现__getitem__方法，定义指定index时如何获取数据，并返回单条数据（训练数据，对应的标签）        """        # row = np.array(self.data[index]).astype('float32')        # predic = np.array(self.label[index]).astype('float32')        # return row, predic        return self.data[index], self.label[index]    def __len__(self):        """        步骤四：实现__len__方法，返回数据集总数目        """        return self.num_samples

登录后复制In [15]

# to_tensorX_train_tensor = paddle.to_tensor(X_train, dtype='float32')  y_train_tensor = paddle.to_tensor(np.array(y_train), dtype='float32')  X_test_tensor = paddle.to_tensor(X_test, dtype='float32')  y_test_tensor = paddle.to_tensor(np.array(y_test), dtype='float32') # 数据导入train_dataset = FlightDataset(X_train_tensor, y_train_tensor)test_dataset = FlightDataset(X_test_tensor, y_test_tensor)# 实例化数据读取器batch_size = 128train_dataloader = paddle.io.DataLoader(train_dataset, shuffle=True, batch_size=batch_size, num_workers=2)test_dataloader = paddle.io.DataLoader(test_dataset, shuffle=False, batch_size=batch_size, num_workers=2)

登录后复制

2. Baseline Model

本项目的Baseline模型是简单的MLP加上一些正则化方式，模型结构见下文summary。
模型最终测试精度为72%。从下图中可以看出模型已存在过拟合现象，因此增加正则化或许能提高模型性能，在此不做深究。

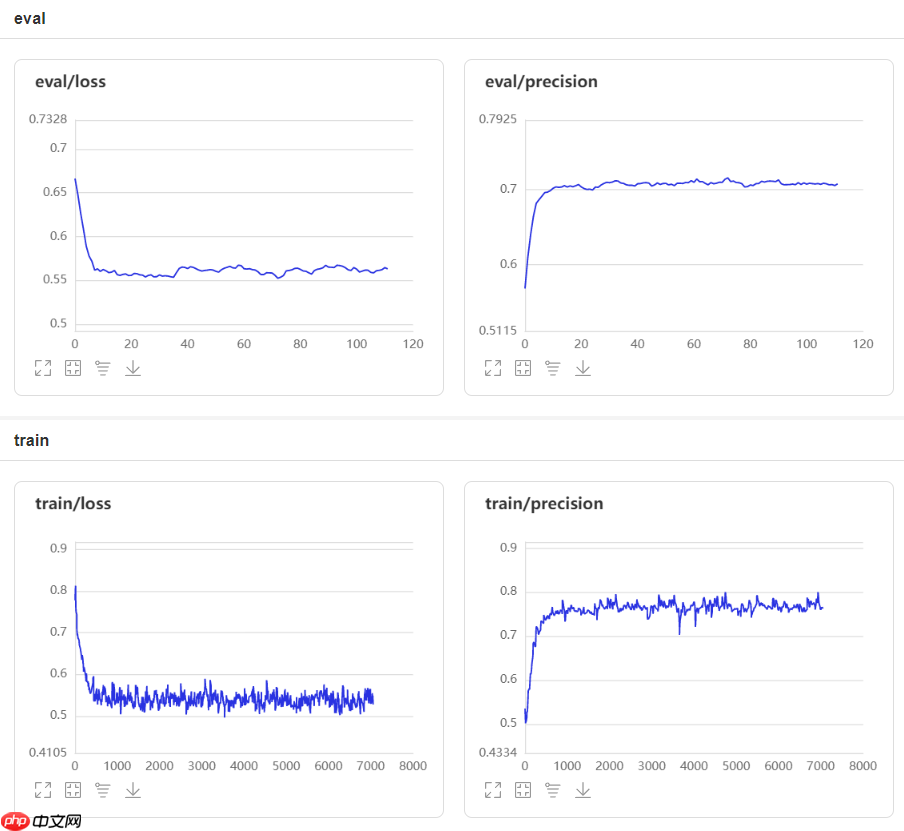
【AI达人特训营】高可信度航班延误预测模型及模型可解释性 - 游乐网

In [16]

# model parametersn_input = X_train.shape[1]n_hidden = 15n_output = 1# define the modelnn_model = nn.Sequential(    nn.Linear(n_input, n_hidden, weight_attr=nn.initializer.KaimingNormal()),     nn.ReLU(),    nn.Dropout(0.5),    nn.Linear(n_hidden, n_hidden, weight_attr=nn.initializer.KaimingNormal()),     nn.ReLU(),    nn.Linear(n_hidden, n_output),     nn.Sigmoid())

登录后复制In [17]

# model summarypaddle.summary(nn_model, (1, 3, 808))

登录后复制

--------------------------------------------------------------------------- Layer (type)       Input Shape          Output Shape         Param #    ===========================================================================   Linear-4        [[1, 3, 808]]          [1, 3, 15]          12,135         ReLU-3          [[1, 3, 15]]          [1, 3, 15]             0          Dropout-2        [[1, 3, 15]]          [1, 3, 15]             0          Linear-5         [[1, 3, 15]]          [1, 3, 15]            240          ReLU-4          [[1, 3, 15]]          [1, 3, 15]             0          Linear-6         [[1, 3, 15]]          [1, 3, 1]             16          Sigmoid-2        [[1, 3, 1]]           [1, 3, 1]              0       ===========================================================================Total params: 12,391Trainable params: 12,391Non-trainable params: 0---------------------------------------------------------------------------Input size (MB): 0.01Forward/backward pass size (MB): 0.00Params size (MB): 0.05Estimated Total Size (MB): 0.06---------------------------------------------------------------------------

登录后复制

{'total_params': 12391, 'trainable_params': 12391}

登录后复制In [ ]

# compile it and run it# compile the modelmodel = paddle.Model(nn_model)learning_rate = 0.001clip = paddle.nn.ClipGradByGlobalNorm(clip_norm=1.0)opt = paddle.optimizer.Adam(learning_rate=learning_rate, parameters=model.parameters(), grad_clip=clip, weight_decay=0.05)model.prepare(optimizer=opt, loss=paddle.nn.BCELoss(), metrics=paddle.metric.Precision())# trainearly_stop = paddle.callbacks.EarlyStopping(monitor='precision', mode='max', patience=50, verbose=0, save_best_model=True)visualdl = paddle.callbacks.VisualDL('log/baseline')model.fit(train_dataloader, test_dataloader, epochs=500, verbose=1,                         callbacks=[early_stop,visualdl], save_dir='checkpoint/baseline', save_freq=50)

登录后复制In [25]

# evaluate baseline modelbest_model = paddle.Model(nn_model)best_model.load('checkpoint/baseline/best_model.pdparams')learning_rate = 0.001clip = paddle.nn.ClipGradByGlobalNorm(clip_norm=1.0)opt = paddle.optimizer.Adam(learning_rate=learning_rate, parameters=best_model.parameters(), grad_clip=clip, weight_decay=0.1)best_model.prepare(optimizer=opt, loss=paddle.nn.BCELoss(), metrics=paddle.metric.Precision())best_model.evaluate(test_dataloader, verbose=0)

登录后复制

{'loss': [0.5625631], 'precision': 0.7204968944099379}

登录后复制

3. Model Interpretation

这到了本项目第一个重点，如何对模型做出解释？

3.1. Feature Importance

第一个方法

为了解释最终的baseline model，我们将首先使用一个我们知道如何解释的“代理模型”，并用我们的baseline模型的预测结果上训练它。

为此我们需要修改我们的训练集。首先，为训练集生成一组baseline model的预测结果。对于“代理模型”的数据集：(a)X与baseline训练集的X相同，(b)将y替换为baseline model对训练集的预测结果。

接下来，用修改后的训练数据集拟合一个logistics regression model(代理模型)。打印代理模型的测试精度以确认它与我们的baseline model测试精度相似。为了达到类似的精度，可能需要调整LogisticRegression中的C。

最后使用sklearn的permutation_importance函数来计算特征的重要性。并生成一个条形图，展示使用permutation_importance得到的前10个最重要的预测因子的相对重要性。

Resource:

permutation_importance 1permutation_importance 2In [21]

# generate logreg dataset# Convert probabilities into labels# 切记不要用train_dataloader来predict，因为有shuffley_train_hat = best_model.predict(X_train_tensor, stack_outputs=True, verbose=0)[0]y_train_logreg = np.round(y_train_hat).ravel()# Fit the logistic regression modellogreg = LogisticRegression(penalty='l2', max_iter=1000)logreg.fit(X_train, y_train_logreg)# Print the logreg test accuracyy_test_logreg_hat = logreg.predict(X_test)print("logreg_model_test_acc:", accuracy_score(y_test_logreg_hat, y_test))

登录后复制

logreg_model_test_acc: 0.7265

登录后复制In [23]

# 需要时间较长(4核需3分钟)# compute the feature importances use permutation_importanceperm_results  = permutation_importance(logreg, X_test, y_test, n_jobs=1)# calculate relative importance of top 10 predictors in descending orderrelimp10 = np.flip(np.sort(perm_results.importances_mean)[-10:])/perm_results.importances_mean.max()# identify indices of top 10 predictors in descending orderrelimp10_idx = np.flip(np.argsort(perm_results.importances_mean)[-10:])# identify top 10 predictor names based on sorted top 10 indicesrelimp10_preds = [X.columns[i] for i in relimp10_idx]

登录后复制In [40]

# plot results of top 10 predictorsfig, ax = plt.subplots(figsize=(9, 6))plt.title(    "Top 10 predictors by relative importance\n"    "as identfied using \"permutation_importance\"",    fontsize=16,)ax.barh(relimp10_preds[::-1], relimp10[::-1], alpha=0.5)ax.tick_params(labelsize=12)ax.set_xlabel("relative feature importance", fontsize=12)ax.grid(':', alpha=0.4)plt.tight_layout()plt.show()

登录后复制

登录后复制登录后复制

3.2. Visualize Important Features

第二种方法

另一种解释的方法是将数据集中除选中的特征外，其他特征全部设置为平均值，以此来观察选中变量对预测结果的影响。需要注意的是，我们最好从上面发现的最重要的特征中选择（SCHED_DEP_HOUR， FLIGHT_COUNT， SCHED_ARR_HOUR， DISTANCE）。为了便于解释，以下所有图的预测因子按其原始比例显示。

In [53]

# examining the response as a function of any of the predictorsdef predictors_examining_14(examining_predictors, NN_model):    '''    input:        examining_predictors: list of strings, the names of the predictors to examine        NN_model: the trained model    output:        None(just print the plot)    '''    # set all predictors to their means of scaled values except the examining variables    # get the original data    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=111)    # get the column index of the examining variables    examining_predictors_index = X_train.columns.get_indexer(examining_predictors)        # scale the data and get the mean of the scaled data    scaler_temp = StandardScaler()    X_train_temp = scaler_temp.fit_transform(X_train)    X_train_final = X_train_temp.copy()    X_train_final[:]= X_train_temp.mean(axis=0)    # keep the examing variables to their scaled values    X_train_final[:,examining_predictors_index] = X_train_temp[:,examining_predictors_index]    X_train_final = paddle.to_tensor(X_train_final, dtype='float32')      # predict the probability of delay with the new data    y_train_hat = NN_model.predict(X_train_final, verbose=0)    # plot the predicted probabilities of delay vs. examining predictors on the training set.    # set the first axis    fig, ax1 = plt.subplots(figsize=(9, 6))    # ax1.set_title('Predicted Probability of Delay vs. '+' & '.join(examining_predictors), fontsize=24)    ax1.set_title(        "\"Model\" training predictions\nby {}\n"\        "with all other predictors are held constant at their means"        .format(            ' & '.join(examining_predictors),        ),        fontsize=15,    )    ax1.set_xlabel('Predicted Probability of Delay', fontsize=16)    ax1.set_ylabel('Original '+examining_predictors[0], color='b', fontsize=16)    s1 = ax1.scatter(y_train_hat, X_train[examining_predictors[0]], c='b', marker='o', label=examining_predictors[0])    ax1.tick_params(axis='y', labelcolor='b')    # set the second axis(if have more than one examining variables)    if len(examining_predictors) == 1:        ax1.legend(loc=0, fontsize=12)        plt.show()    else:        # Create a second Y-axis that shares the X-axis        ax2 = ax1.twinx()        ax2.set_ylabel('Original '+examining_predictors[1], color='r', fontsize=16)        s2 = ax2.scatter(y_train_hat, X_train[examining_predictors[1]], c='r', marker='o', label=examining_predictors[1])        ax2.tick_params(axis='y', labelcolor='r')        # Add the legend to the plot        sca = [s1,s2]        labels = [lable.get_label() for lable in sca]        plt.legend(sca, labels,loc = 2, fontsize=12)        plt.show()

登录后复制In [54]

# except SCHED_DEP_HOUR (3.2.1)predictors_examining_14(['SCHED_DEP_HOUR'], best_model)

登录后复制

登录后复制登录后复制

通过保持所有其他变量不变，我们可以观察到SCHED_DEP_HOUR对模型预测结果的影响。可以看到，随着一天中预定起飞时间的增加，航班延误的预测概率也会增加。这一发现有助于说明了该变量在我们的模型中的影响。然而，这一发现也提出了一些问题，即其他哪些混杂因素可能导致这一预测的影响。下面将探究变量之间的影响。

In [55]

# except SCHED_DEP_HOUR and FLIGHT_COUNT (3.2.2)predictors_examining_14(['SCHED_DEP_HOUR','FLIGHT_COUNT'], best_model)

登录后复制

登录后复制登录后复制登录后复制In [56]

# except SCHED_DEP_HOUR and SCHED_ARR_HOUR (3.2.3)predictors_examining_14(['SCHED_DEP_HOUR','SCHED_ARR_HOUR'], best_model)

登录后复制

登录后复制登录后复制登录后复制In [57]

# except SCHED_DEP_HOUR and DISTANCE (3.2.4)predictors_examining_14(['SCHED_DEP_HOUR','DISTANCE'], best_model)

登录后复制

登录后复制登录后复制登录后复制

上面三张图最明显的是，"SCHED_DEP_HOUR"对预测结果的影响显著大于另一个对比的变量，这与上面得到的feature importance结果一致。表明模型预测结果主要受该变量影响。
在3.2.2中，每天的航班数量可以集中在0-300的范围内，延误的概率随着航班数量的增加而略有增加。由此可以推断出，繁忙的机场会增加延误的概率。
在3.2.3中，随着到达时间从0增加到24，延误概率略有增加，需要注意的是，右下角的点是第二天到达的（延误概率高主要是受前一天出发时间晚的影响）。
在3.2.4中，我们可以看到，飞行距离集中在0到3000英里之间，随着飞行距离的增加，延误概率也略有增加。

4. Bagging (bootstrap-aggregated)

这是该项目的第二个重点

这里使用与baseline model相同的网络架构(层、节点、激活等)，使用bootstrap创建多个训练集，并为每个bootstrap数据集拟合一个单独的MLP模型。预测每个模型的测试数据的输出。

Resource：

https://www.zhihu.com/column/p/262211315https://blog.csdn.net/dmsgames/article/details/81943206

In [60]

def progressbar(n_step, n_total):    """Prints self-updating progress bar to stdout to track for-loop progress        There are entire 3rd-party libraries dedicated to custom progress-bars.    A simple function like this is often more than enough to get the job done.        :param n_total: total number of expected for-loop iterations    :type n_total: int    :param n_step: current iteration number, starting at 0    :type n_step: int    .. example::            for i in range(n_iterations):            progressbar(i, n_iterations)                .. source:            This function is a simplified version of code found here:        https://stackoverflow.com/questions/3160699/python-progress-bar/15860757#15860757    """    n_step = n_step + 1    barlen = 50    progress = n_step / n_total    block = int(round(barlen * progress))    status = ""    if n_step == n_total:        status = "Done...\r\n\n"    text = "\r [{0}] {1}/{2} {3}".format(        "=" * block + "-" * (barlen - block),        n_step,        n_total,        status,    )    sys.stdout.write(text)    sys.stdout.flush()

登录后复制In [62]

# build and compile the modeldef buildModel(learning_rate = 0.001):    '''    input:    learning_rate: float, the learning rate of the model    output:    model: the model    '''    # build NN model    # model parameters    n_input = X_train.shape[1]    n_hidden = 15    n_output = 1    # define the model    nn_model = nn.Sequential(        nn.Linear(n_input, n_hidden, weight_attr=nn.initializer.KaimingNormal()),         nn.ReLU(),        nn.Dropout(0.5),        nn.Linear(n_hidden, n_hidden, weight_attr=nn.initializer.KaimingNormal()),         nn.ReLU(),        nn.Linear(n_hidden, n_output),         nn.Sigmoid()    )    # compile the model    model = paddle.Model(nn_model)    clip = paddle.nn.ClipGradByGlobalNorm(clip_norm=1.0)    opt = paddle.optimizer.Adam(learning_rate=learning_rate, parameters=model.parameters(), grad_clip=clip, weight_decay=0.05)    model.prepare(optimizer=opt, loss=paddle.nn.BCELoss(), metrics=paddle.metric.Precision())    return model

登录后复制In [ ]

%%time# 需要时间较长(4核需xx分钟)# bootstraps不应过小，否则体现不出效果# bootstraps数量与训练时间成正比，可以通过减小bootstraps缩短学习时间# Bootstrap and train your networks and get predictions on fixed X test databootstraps = 100epochs = 500batch_size = 256learning_rate = 0.001boot_models = []for i in range(bootstraps):    # progress bar    progressbar(i, bootstraps)    # build, compile and train the model    boot_X_train, boot_y_train = resample(X_train, y_train, replace=True, n_samples=int(X_train.shape[0]))    boot_model = buildModel(learning_rate=learning_rate)    # generate resample dataset    boot_X_train = paddle.to_tensor(boot_X_train, dtype='float32')      boot_y_train = paddle.to_tensor(np.array(boot_y_train), dtype='float32')    boot_train_dataset = FlightDataset(boot_X_train, boot_y_train)      boot_train_dataloader = paddle.io.DataLoader(boot_train_dataset, shuffle=True, batch_size=256, num_workers=4)    early_stop = paddle.callbacks.EarlyStopping(monitor='precision', mode='max', patience=50, verbose=0, save_best_model=True)    boot_model.fit(boot_train_dataloader, test_dataloader, epochs=epochs, verbose=0, callbacks=[early_stop])    # save model    boot_models.append(boot_model)

登录后复制

4.1. Confidence Interval

随机选择6个测试观测数据，在6个子图上绘制预测概率的分布(即n个bootstrapped probability)，在每个子图中标记95%CI边界，在每个子图的标题中包含每个观测数据的实际类别，以便于参考。

根据下面显示的6个图可以观察到一些有趣的东西，大部分情况下，无论使用的是何种bootstrap数据集，该模型都可以"自信"的预测出结果。这意味着，大多数概率预测都处于产生“正确”的预测(p= 0.5的一侧)。我们也可以观察到其中模型预测错误的情况，也非常"自信"。其他的测试预测似乎远没有那么确定，在这些情况下，bootstrap预测的分布更加分散。

In [147]

# ramdomly select 10 test observationsboot_X_test, boot_y_test = resample(X_test, y_test, replace=0, n_samples=6)boot_y_hat = np.zeros((bootstraps, boot_X_test.shape[0]))for i in range(bootstraps):    boot_y_hat[i] = boot_models[i].predict(paddle.to_tensor(boot_X_test, dtype='float32') , stack_outputs=True, verbose=0)[0].ravel()boot_y_hat = boot_y_hat.T

登录后复制In [148]

# plot the distribution of predicted probabilities with the 95% CI bounds clearly marked and reported in each subplotfig, ax = plt.subplots(6, 1, figsize=(9, 25))for i in range(6):    ax[i].set_title(f'The distribution of {bootstraps} bootstrapped probabilites with the 95% CI bounds , sample {i}, True label: {boot_y_test.iloc[i]}')    ax[i].hist(boot_y_hat[i], bins=30, range=(0, 1), color='blue')    ax[i].axvline(boot_y_hat[i].mean(), color='k', linestyle='dashed', linewidth=2, label='Mean')    ax[i].axvspan(np.percentile(boot_y_hat[i], 2.5), np.percentile(boot_y_hat[i], 97.5), color='red', alpha=0.3, label='95% CI')    ax[i].set_xlabel('Predicted Probability of Delay')    ax[i].set_ylabel('Frequency')    ax[i].legend()fig.tight_layout()plt.show()

登录后复制

4.2. Abstain Model

使用从上面的bootstrap样本中获得的预测的概率分布，我们可以评估我们的bagging(即bootstrap-aggregated)预测对每个测试观察的“重要性”。为了实现这一点，首先计算跨越阈值p=0.5的bootstrapped的比例。我们称这个比例为PPR(Posterior Prediction Ratio)。当PPR=0时，该条数据(一行数据)的所有bootstrap概率都在p=0.5的同一侧。同样地，当PPR=0.5时，该条数据(一行数据)的bootstrap预测的一半是y=0，另一半是y=1。在计算所有测试观察值后，应该有 2000个PPR值(即每条数据一个PPR值)。

接下来，为了获得更准确的预测，我们可以创建一个Abstain Model，如果未满足某个定义的显著性阈值(即最大PPR值)，该模型将不会对某一行数据进行预测。

最后，绘制出abstain bagging model中未弃权的测试观察结果的比例(即有预测结果的比例)，以及预测准确的比较。

最后的图中显示，随着PPR阈值的减小(更高可信度)，有预测结果的比例有明显下降。反之，预测比例上升。我们还可以看到，在更低的PPR阈值下，我们的分类准确率越来越高。而我们abstain bagging model所能做到的最好的情况是在牺牲50%的可用预测的基础上，将测试精度增加约10个额外点。

In [149]

# predict all test data with the bootstrapped modelsboot_y_hat_all = np.zeros((bootstraps, X_test.shape[0]))for i in range(bootstraps):    # progress bar    progressbar(i, bootstraps)    # predict    boot_y_hat_all[i] = boot_models[i].predict(X_test_tensor, stack_outputs=True, verbose=0)[0].ravel()boot_y_hat_all = boot_y_hat_all.T# calculate posterior prediction ratioboot_y_hat_label = np.round(boot_y_hat_all)PPR = (boot_y_hat_label==0).mean(axis=1)

登录后复制

 [==================================================] 100/100 Done...

登录后复制In [150]

def abstain_bagging_model(threshold=0.5):    '''    input:        threshold: float, max is 0.5, when it is 0 the bagging model have 100% confidence    output:        The rest of the samples, accuracy and proportion of the samples that not abstained    '''    # delete the abstained samples    indexes = np.where(abs(PPR-0.5) >= abs(threshold-0.5))    X, y = X_test[indexes], y_test.iloc[indexes]    # calculate the proportion of the samples that not abstained    proportion = X.shape[0]/X_test.shape[0]    # calculate the accuracy    acc = ((np.round(boot_y_hat_all[indexes]).sum(axis=1)>(len(boot_models)/2))==y_test.iloc[indexes]).mean()    return X, y, acc, proportion

登录后复制In [151]

# test accuracy and proportion of test observations not abstained for abstain bagging modeldef  plot_acc_proportion_16(start, end, step):    '''    input:        start: the start of the range        end: the end of the range        step: the step of the range    output:        plot the accuracy and proportion of the samples that not abstained    '''    # generate the data for the next part    arr = np.arange(start, end, step)    accs=[]    pros=[]    for i in arr:        _, _, acc, proportion = abstain_bagging_model(threshold=i)        accs.append(acc)        pros.append(proportion)    # plot accuracies and proportion of test observations not abstained for abstain bagging model        # plot accuracies    # set the first axis    fig16, ax16 = plt.subplots(figsize=(14,7))    ax16.set_title('PPR Threshold vs. Accuracy and Rest Propotion of Test Observation', fontsize=24)    ax16.set_xlabel('Posterior Prediction Ratio Threshlod', fontsize=16)    ax16.set_ylabel('Accuracy of abstain bagging model', color='b', fontsize=16)    s1 = ax16.plot(arr, accs, c='b', label='Accuracy')    ax16.tick_params(axis='y', labelcolor='b')    ax16.legend(loc=0)    # plot the proportion of test observations not abstained    # Create a second Y-axis that shares the X-axis    ax2 = ax16.twinx()    ax2.set_ylabel('Rest ratio of test observation', color='r', fontsize=16)    s2 = ax2.plot(arr, pros, c='r', label='Rest Propotion')    ax2.tick_params(axis='y', labelcolor='r')    ax2.legend(loc=0)    # # fig16.tight_layout()    plt.show()

登录后复制In [152]

# test accuracy and proportion of test observations not abstained for abstain bagging model when the threshold is increasedplot_acc_proportion_16(0, 0.51, 0.01)

登录后复制