几何画板解圆上动点到直线距离最值问题
圆上动点到直线距离的最值问题是高考中常见的题型，主要考查学生的转化思想与数形结合能力。在教学实践中，如何通过直观的方式帮助学生理解这一知识点，并引导他们用数学思维观察、分析和表达现实世界，具有重要意义。我们借助几何画板解决此类问题，不仅能够形象展示动态变化过程，还能即时验证结果，有效提升了学习效率。以下分享具体操作经验：
免费影视、动漫、音乐、游戏、小说资源长期稳定更新！ 👉 点此立即查看 👈
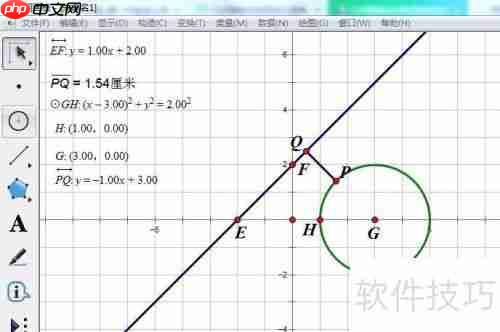
以(3,0)为圆心，2为半径作圆。
绘制直线y=x+2。
在圆上取一动点P，向直线作垂线，垂足记为Q。
测量PQ的长度。
如图所示，5月28日
拖动点P沿圆周运动。
Q点随之发生变化。
可以观察到PQ的长度不断变化，有时增大，有时减小。
如图所示，当P点处于特定位置时，
PQ长度达到最大值5.54。
此时发现PQ经过圆心，并且圆心是PQ线段的内分点。
因此我们提出一个猜想：
当PQ过圆心，且圆心为PQ线段的内分点时，PQ长度取得最大值5.54。
接下来验证这个假设是否成立。
过圆心G作直线y=x+2的垂线，求得其方程为y=-x+3，标记该垂线为PQ。
发现该垂线恰好经过点P，说明猜想正确。
参照第5步的操作，再次观察数据，
提出另一个猜测：PQ最小值为1.54。
此时PQ仍经过圆心，但圆心变为PQ线段的外分点。
得出新的猜想：
当PQ过圆心，且圆心为PQ线段的外分点时，PQ长度取得最小值1.54。
验证该猜想：
再次过圆心G作直线y=x+2的垂线，得到方程y=-x+3，标记为PQ。
发现该垂线确实经过点P，因此猜想成立。
热门专题
热门推荐
卡达诺生态的下一站：从研发深水区驶向规模化蓝海 区块链世界从不缺少雄心，但能将蓝图一步步变为现实的玩家却不多。近期，卡达诺核心开发团队Input Output Global（IOG）发布了一份面向2030年的网络可扩展性战略，目标明确：将网络每月交易处理能力从当前的80万笔，大幅提升至2700万笔。
企业加密货币钱&包：在便捷与安全之间找到你的平衡点 数字化浪潮下，企业如何安全、高效地管理数字资产，成了一个绕不开的核心议题。企业加密货币钱&包，正是为此而生的专业工具。它远不止一个存储地址那么简单，更是集成了多用户权限、交易审批、财务系统对接等企业级功能的管理中枢。简单来说，它的核心任务就两个：安
PhpStorm配置GitHub Copilot：AI辅助编程插件安装与使用 PhpStorm里装不上GitHub Copilot？先确认IDE版本和插件源 如果你在PhpStorm里死活装不上GitHub Copilot，问题大概率出在版本上。一个关键前提是：PhpStorm 2023 3及之后的
Notepad++宏录制需先打开文档（如Ctrl+N新建标签），否则按钮灰色禁用；仅捕获键盘操作与部分菜单命令，不支持鼠标、对话框交互；录制后须手动导出XML保存，否则重启丢失。 怎么开始录制宏却没反应？ 很多朋友第一次用Notepad++的宏功能，都会遇到一个经典问题：那个“开始录制”的按钮，怎么
Ordinals (ORDI) 深度展望：2026-2030，百倍增长是神话还是可期的未来？ 加密货币市场从不缺少惊喜，而Ordinals协议及其原生代币ORDI的异军突起，无疑是近年来最引人注目的叙事之一。这项技术巧妙地将数据“铭刻”在比特币的最小单位——“聪”上，硬生生在价值存储的基石上，开辟出